Основные характеристики стохастических сетей

1. Число n систем массового обслуживания S₁,.., Sn, образующих сеть.

2. Число каналов (обслуживающих приборов) k₁,.., k_n, входящих в системы S₁,.., S_n.

3. Матрица вероятностей передач P = [Pij], где Pij - вероятность того, что заявка, покидающая систему Si поступит в систему Sj (i, j = 0,.., n).

4. Число M заявок, циркулирующих в замкнутой сети.

5. Интенсивность источника заявок S₀ в разомкнутой сети.

6. Среднее время обслуживания заявок v₁,.., v_n в системах S₁,.., S_n.

Т.к. в сети заявки не теряются, и заявка, выходящая из системы Si обязательно попадёт в другую систему Sj, то должно выполняться условие:

=> сумма элементов строки матрицы равна 1, т.е. матрица стохастическая.

- Среднее число заявок, поступивших в систему Si за некоторый промежуток времени равно среднему числу заявок, покинувших эту систему, т.е. интенсивности входящего и выходящего потоков для системы Si равны между собой.

Т.к. заявки из Sj поступают в Si с вероятностью Pji, => интенсивность потока из Sj в Si равна Pji, где - интенсивность выходящего и, следовательно, входящего потока заявок Sj.

Отсюда следует, что на входе системы Si имеется поток с интенсивностью

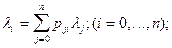(17.1)

Получаем систему уравнений (n + 1)-го порядка в канонической форме:

Из системы (17.2) определим соотношение интенсивностей потоков

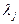и в виде .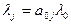

Коэффициент a_0j называется коэффициентом передачи и определяет среднее число этапов обслуживания в системе Sj одной заявки, поступающей от источника S₀.

Будем обозначать a a₀ = 1.

Для разомкнутых сетей известна величина и => система (17.2) имеет единственное решение.

Для замкнутых сетей система (17.2) имеет бесконечное число решений, тогда коэффициент a_j определяется при = 1.

Пример 1. Разомкнутая сеть.

Определить интенсивность 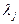и коэффициенты передач a _j для разомкнутой сети.

Пусть ; p₁₀ = 0.1, p₁₂ = 0.4, p₁₃ = 0.5.

По (7.1) получим:

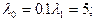
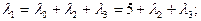
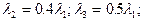
Дата добавления: 2014-01-13