Теорема Джексона

Упрощенные модели СОО

Сетевая модель СОО с

Замкнутая модель СОО неограниченным числом заявок

P₁

S₀

S₁

P

T₁ S₁

ПР-ОП

p₂

S₂

T_M

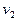
S_n

p_n

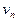
Рис.18.4 Рис. 18.5.

Разомкнутая стохастическая сеть с простейшим входным потоком и экспоненциальным обслуживанием в каждом элементе сети распадается на отдельные системы, которые могут анализироваться независимо от других (рис.18.6).

Матрица вероятностей

Передач

p 0 1 2... n

0 0 1 0... 0

1 p₁ p₂ 1 p p₁ p₂... p_n

2 0 1 0... 0

S₀ S₁ S₂ p=........

........

n 0 1 0... 0

p_n

S_n

Рис.18.6.

Определение :

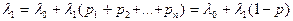(18.1)

из (18.1):

Коэффициенты передач a1 =1/p, ai =pi/p - это количество этапов обслуживания заявок в системах S1,...,Sn.

ti = ai - время, в течение которого заявка находится в

системе Si.

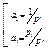
Определим среднее время пребывания заявки в i-м узле системы:

t1 = /p -среднее процессорное время;

ti =(pi/p) -время обмена через СК.

Определим параметр, равный отношению среднего суммарного времени выполнения операций обмена через СК для одной задачи к среднему процессорному времени, требуемому для ее решения:

yi = ti / t1.

Определяем загрузку устройств Si через yi и определяем вероятности P(Li),

где Li -среднее число заявок в системе Si, равное сумме средней длины очереди li и среднего числа занятых каналов ki.

Li = li + ki.

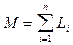- глубина мультипрограммирования.

Определим среднее время пребывания заявок в сети (среднее время ответа на заявки пользователей):

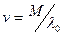, но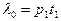=>- среднее нормированное время

M ответа на заявки пользователей равно

отношению среднего значения

коэффициента мультипрограммирования

к загрузке процессора.

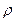Для однопроцессорной системы y2 =t2 / t1.

Рис.18.7.

Среднее значение коэффициента мультипрограммирования M->min при t2 = 0, т.е. когда среднее время выполнения всей операции обмена равно 0, или при t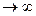(т.е. среднее процессорное время, необходимое для обработки одного запроса пользователя).

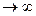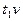
Рис.18.8.

Для СОО с несколькими СК

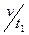
1-1 СК

2-2 СК

3- СК

При 2-х СК среднее нормированное время

ответа близко к времени ответа при

нескольких СК.

Рис.18.9.

-интенсивность входного потока,

-среднее время обслуживания в одном канале,

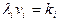-среднее число занятых каналов.

, где Ki -общее число каналов системы i.

Стационарный режим:

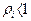, т.к 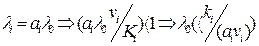. -ограничение на входной поток.

Дата добавления: 2014-01-13