
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Уравнение Бернулли для потока реальной жидкости
|
|
|
|
Пусть поток реальной жидкости, обладающей вязкостью, движется в русле, ограниченном неподвижными стенками. При этом возникает трение, что приводит к существенной неравномерности распределения скоростей по сечению потока (рис. 3.5), а также к потерям энергии при перемещении жидкости от одного сечения к другому.
Получим уравнение Бернулли для потока реальной жидкости, основываясь на том, что оно является законом сохранения энергии для движущейся жидкости. Вывод этого уравнения проведем в два этапа. На первом этапе учтем неравномерность распределения скоростей по сечению потока, а на втором учтем и потери энергии.
При выводе будем считать, что в пределах выбранных сечений
гидростатический напор остается постоянным:
Z + = const. (3.7)
= const. (3.7)

Рис. 3.5. Схема потока реальной жидкости
Это справедливо для сечений с параллельно струйным течением жидкости, т.е. когда эти сечения являются плоскими. Поэтому уравнение которое будет получено ниже, может использоваться для плоских или близких к ним сечений.
На первом этапе определим формулу для вычисления мощности N потока реальной жидкости в его сечении. Вычисление этого параметра затруднено тем, что из-за перераспределения скоростей (см. рис. 3.5) разные слои жидкости несут различное количество энергии. Для определения мощности N в сечении (например, в сечении 1— 1 на рис. 3.5) выберем струйку жидкости бесконечно милой поперечной площади dS, в пределах которой скорость жидкости будем считать постоянной, равной v. Тогда полный напор (или полная удельная энергия) в сечении струйки
H=Z+ 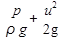 (3.8)
(3.8)
Мощность струйки dN в сечении площадью dS равна произведению удельной энергии Н и веса жидкости, которую проносит поток через это сечение в единицу времени, т.е. элементарного носового расхода dQG. Тогда с учетом (3.6) и (3.1) получим математическую зависимость для мощности струйки
dN=GdQg=(Z+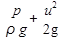 )pgdQ (3.9)
)pgdQ (3.9)
Мощность всего потока в сечении найдем, просуммировав мощности всех элементарных струек, т.е. вычислив интеграл по площади S от выражения (3.9):
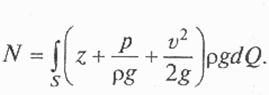
После математических преобразований зависимость для мощности потока реальной жидкости принимает следующий вид:
N=pg(z+ )Q (3.10)
)Q (3.10)
где α — безразмерный коэффициент, определяемый по формуле
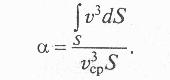 (3.11)
(3.11)
Этот коэффициент, называемый коэффициентом Кориолиса, учитывает неравномерность распределения скорости жидкости сечении реального потока. Если числитель и знаменатель в формуле (3.11) умножить на р/2, то станет очевидно, что коэффициент а есть отношение действительной кинетической энергии реального потока в данном сечении к кинетической энергии того же потока в том же сечении, но посчитанной по средней скорости жидкости в данном сечении. В этом заключается физический смысл коэффициента Кориолиса.
Алгебраическое выражение, ограниченное скобками в (3.10), принято называть средним значением полного напора в сечении реального потока, т.е.
Hср=z+ (3.12)
(3.12)
Средний напор Hср широко используется в практических расчетах, так как является важнейшим параметром, характеризующим механическую энергию (или мощность) потока реальной жидкости. Для подтверждения этого решим уравнение (3.10) относительно Hср с учетом (3.12). Тогда получим
Hср=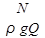 . (3.13)
. (3.13)
Из анализа зависимости (3.13) следует, что при постоянном расходе Q средний напор Hср пропорционален мощности N ив пределах данного потока однозначно определяет эту мощность. Поэтому средний напор Hср, вычисляемый с учетом неравномерности распределения скоростей в сечении по формуле (3.12), в дальнейшем будем использовать в качестве основного параметра, характеризующего механическую энергию потока реальной жидкости.
Учтем теперь потери энергии, возникающие при движении жидкости. В реальных потоках из-за этих потерь среднее значение полного напора в в конечном сечении всегда меньше, чем в начальном сечении, т.е. Hср1 > Нср2. Поэтому при записи уравнения баланса (средних напоров) в его правую часть добавляют слагаете ∑hпот учитывающее потери удельной энергии. Тогда уравнение баланса принимает вид
Hср1 = Нср1 + ∑hпот,
или с учетом (3.12)
z1+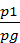 +α1
+α1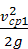 =z2+
=z2+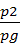 +α1
+α1 +∑hпот (3.14)
+∑hпот (3.14)
Уравнение (3.14) носит название уравнения Бернулли для потока реальной жидкости.
При использовании этого уравнения в дальнейшем индексы «ср» будем опускать. Сравним уравнение Бернулли для струйки идеальной жидкости (3.6) и уравнение для потока реальной жидкости (3.14). Из этого сравнения следует, что в последнем уравнении дополнительно присутсвуют α и ∑hпот.
При равномерном распределении скоростей по сечению потока α=1 (поток идеальной жидкости). В потоках реальной жидкости коэффициент Кориолиса в большинстве случаев лежит в пределах 1<α≤2.
Суммарная потеря полного напора ∑hпот на участке между начальным и конечным сечениями складывается из суммы потерь удельной энергии во всех гидравлических сопротивлениях, расположенных на рассматриваемом участке потока. В гидравлике эти потери энергии принято делить на две группы: местные потери и потери на трение по длине. Местные потери hM — это потери в местных (локальных) гидравлических сопротивлениях, к которым относятся поворот, сужение или расширение потока, а также различные гидравлические устройства (вентили, жиклеры и т.д.). Потери в большинстве этих сопротивлений вызваны вихреобразованием. Как показывает практика, они пропорциональны квадрату скорости жидкости, а для оценки их величины используется формула Вейсбаха
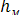 = ζ
= ζ 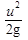 (3.15)
(3.15)
где С, — безразмерный коэффициент, определяющий потери в данном местном сопротивлении; v — средняя скорость в трубопроводе, в котором установлено местное сопротивление.
Второй вид гидравлических потерь — потери на трение по длине 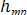 — это потери, которые имеют место в длинных прямых трубах постоянного сечения. Потери на трение по длине вызваны как внутренним трением в жидкости, так и трением о стенки трубы, Эти потери пропорциональны длине трубы l и обратно пропорциональны ее диаметру d. Они имеют достаточно сложную зависимость от средней скорости жидкости v (это будет рассмотрено позднее), но во всех случаях для их оценки может быть использована универсальная для гидравлики формула Дарси
— это потери, которые имеют место в длинных прямых трубах постоянного сечения. Потери на трение по длине вызваны как внутренним трением в жидкости, так и трением о стенки трубы, Эти потери пропорциональны длине трубы l и обратно пропорциональны ее диаметру d. Они имеют достаточно сложную зависимость от средней скорости жидкости v (это будет рассмотрено позднее), но во всех случаях для их оценки может быть использована универсальная для гидравлики формула Дарси
Hтр=λ  (3.16)
(3.16)
где λ — безразмерный коэффициент потерь на трение по длине, который принято называть коэффициентом Дарси.
Следует отметить, что определение потерь энергии при расчете!! гидравлических систем является одной из наиболее важных проблем гидравлики.
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 651; Нарушение авторских прав?; Мы поможем в написании вашей работы!