Идеальные газы

Согласно закону Джоуля, выведенному эмпирически, внутренняя энергия идеального газа не зависит от давления или объёма. Исходя из этого факта, можно получить выражение для изменения внутренней энергии идеального газа. По определению молярной теплоёмкости при постоянном объёме, 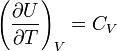. Так как внутренняя энергия идеального газа является функцией только от температуры, то

. (7.30)

Эта же формула верна и для вычисления изменения внутренней энергии любого тела, но только в процессах при постоянном объёме (изохорных процессах); в общем случае C_V (T, V) является функцией и температуры, и объёма.

Если пренебречь изменением молярной теплоёмкости при изменении температуры, получим:

Δ U = ν C_V Δ T, (7.31)

где ν — количеств о вещества, Δ T — изменение температуры.

Термодинамические процессы: изохорный, изобарный, изотермический, адиабатный, политропный

Изохорный процесс (v=const)

Такой процесс может совершаться рабочим телом, находящимся в цилиндре при неподвижном поршне, если к рабочему телу подводится теплота от источника теплоты (см. рис.7.9) или отводится теплота от рабочего тела к холодильнику. При изохорном процессе выполняется условие dv=0 или v=const. Уравнение изохорного процесса получим из уравнения состояния идеального газа при v=const. В pv -координатах график процесса представляет собой прямую линию, параллельную оси p. Изохорный процесс может протекать с повышением давления (процесс 1-2) и с понижением (процесс 1-2’).

Запишем для точек 1 и 2 уравнения состояния: p₁·v=R·T₁; p₂·v=R·T₂. Следовательно, для изохорного процесса

Приращение внутренней энергии газа

Работа газа:

так как dv=0.

Энтальпия газа i_v=u+p·v, а di_v=du+d(p·v)=du+p·dv+v·dp=du+v·dp. Поэтому

Энтропия

То есть

Изобарный процесс (p=const)

В p-v координатах график процесса представляет собой прямую линию параллельную оси v (рис. 7.10). Изобарный процесс может протекать с увеличением объёма (процесс 1-2) и с уменьшением (процесс 1-2’). Запишем для точек 1 и 2 уравнения состояния: p·v₁=R·T₁; p·v₂=R·T₂.

Следовательно, для изобарного процесса

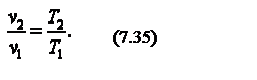
Приращение внутренней энергии газа Работа газа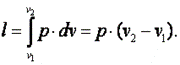

Так как p·v₂=R·T₂, а p·v₁=R·T₁, то l=R·(T₂-T₁). Следовательно, газовая постоянная имеет определённый физический смысл: это работа 1 кг газа в изобарном процессе при изменении температуры на один градус. Следует, что в изобарном процессе q=c_p·(T₂-T₁). В соответствии с первым законом термодинамики для изобарного процесса можно записать dq=du+p·dv= du+d(p·v)=di. Поэтому в изобарном процессе di=q=c_p·(T₂-T₁). Из соотношений, характеризующих изобарный процесс, вытекает известное уравнение Майера. Так как dq=c_p·dT=c_v·dT+dl=c_v·dT+R·dT, то R=c_p-c_v.

Можно показать, что в изобарном процессе энтропия газа

Изотермический процесс (T=const)

В p-v координатах график процесса изображается равнобокой гиперболой (рис. 7.11). Изотермический процесс может протекать как с увеличением объёма (процесс 1-2), так и с уменьшением объёма (процесс 1-2’).

Запишем для точек 1 и 2 уравнения состояния p₁·v₁=R·T; p₂·v₂=R·T. Следовательно, для изотермического процесса p₁·v₁=p₂·v₂=const.

Приращение внутренней энергии газа:

Работа газа

Теплота, подводимая в процессе

Изменение энтальпии газа Δi=Δu+Δ(p&middotv)=0.

Изменение энтропии газа

Адиабатный процесс

Адиабатный процесс – это процесс, при котором рабочее тело не обменивается теплотой с окружающей средой (dq=0). Для получения графика процесса в p-v координатах выполним некоторые преобразования.

В соответствии с первым законом термодинамики, где с – теплоёмкость термодинамического процесса. Тогда можно записать, что

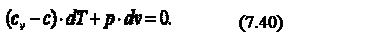
Продифференцируем уравнение состояния идеального газа и запишем

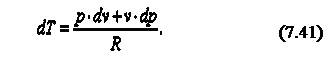
Так как R=c_p-c_v, то выражение (7.41) можно переписать с учётом (7.42) следующим образом:

Выполним преобразования выражения

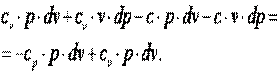
(7.44)

(7.45)

Разделим выражение (7.44) и получим:

Обозначим , тогда

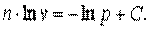
Следовательно

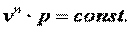
(7.46)

В адиабатном процессе dq=0, то есть c&middotdT=0. Поэтому c=0. Значит в адиабатном процессе 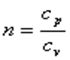. Эту величину принято обозначать буквой 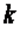и называть показателем адиабаты.

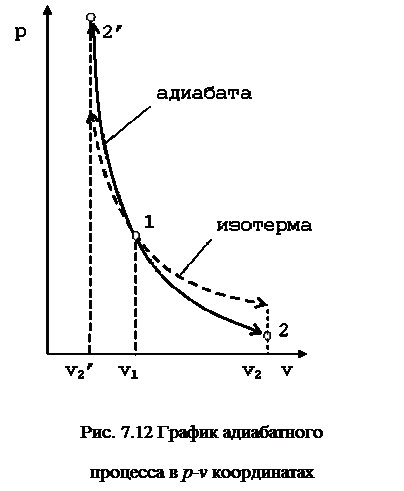Поэтому в p-v координатах адиабатный процесс изображается неравнобокой гиперболой v^k&middotp=const (рис. 7.12). Так как k>1, то адиабата проходит круче гиперболы. Адиабатный процесс может протекать как с увеличением объёма (процесс 1-2), так и с уменьшением объёма (процесс 1-2’).

Запишем для точек 1 и 2 уравнения состояния Так как в адиабатном процессе p₁&middotv₁^k=p₂&middotv₂^k, то , , .

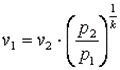Приращение внутренней энергии газа.

Так как 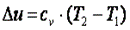, а , то , а .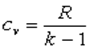

Поэтому

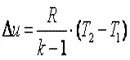
(7.47)

Работа газа в адиабатном процессе выполняется за счёт его внутренней энергии. Так как в адиабатном процессе отсутствует обмен теплотой с окружающей средой, то в соответствии с первым законом термодинамики имеем l+Δu=0 или l=-Δu. Поэтому

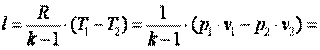
(7.48)

Изменение энтальпии газа в адиабатном процессе может быть определено исходя из следующих соображений:

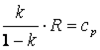
Так как, то в итоге получим

Энтропия газа в адиабатном процессе не изменяется, так как dq=0. Поэтому в T-s координатах адиабатный процесс изображается прямой линией, параллельной оси температур.

Политропный процесс

Политропным процессом называется любой произвольный процесс изменения состояния рабочего тела, происходящий при постоянной теплоёмкости с_п.

Для получения графика политропного процесса в p-v координатах будем придерживаться тех же рассуждений, что и при получении графика адиабатного процесса. Заменим в соотношениях, полученных при изучении адиабатного процесса, обозначение теплоёмкости с на с_п и обнаружим, а 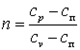. В дальнейшем всё, что написано об адиабатном процессе, можно распространить на описание политропного процесса, заменяя в выражениях k на n.

Покажем, что адиабатный процесс делит все процессы на две группы: на процессы, в которых теплоёмкость больше нуля, и на процессы, в которых теплоёмкость меньше нуля.

Так как 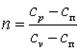, то можно записать

;

;

;

.

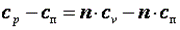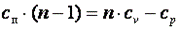Из последнего выражения видно, что при n>k c_п>0, а при k>n>1 c_п<0.

В заключение отметим, что все рассмотренные ранее процессы – это частные случаи политропного процесса.

При n=k имеем адиабатный процесс.

При n=0 имеем р₁·v₁⁰=р₂·v₂⁰, то есть изобарный процесс (p₁=p₂).

При n=1 имеем р₁·v₁= р₂·v₂, то есть изотермический процесс.

При n=∞ имеем

или , что равносильно

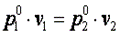
или 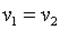, то есть изохорный процесс.

Дата добавления: 2014-01-13