
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные понятия. Лекция 2. Элементы теории множеств
|
|
|
|
Лекция 2. Элементы теории множеств.
Элементарная математика
Основные понятия, включенные в систему тренинг-тестирования:
множество; элемент множества; числовые множества; конечные множества; бесконечные множества; подмножества; пустое множество; объединение множеств; пересечение множеств; разность множеств; симметрическая разность множеств; декартово произведение множеств; отображение; образ; прообраз; сюръективное отображение; инъективное отображение; биективное отображение; мощность множества.
Множество – одно из важнейших понятий математики. Вводится аксиоматически и не может быть определено через какие-либо элементарные понятия.
Кантор описывает множество следующим образом:
Множество 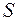 есть любое собрание определенных и различимых между собой объектов нашей интуиции и интеллекта, мыслимое как единое целое. Эти объекты называются элементами множества
есть любое собрание определенных и различимых между собой объектов нашей интуиции и интеллекта, мыслимое как единое целое. Эти объекты называются элементами множества 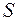
Термин множество характеризует совокупность, объединение некоторых объектов произвольной природы – элементов множества, которые обладают каким-либо общим для них свойством (признаком). Этот общий признак содержится в самом названии (задании) множества. Множество состоит из элементов и считается заданным, если о каждом из рассматриваемых объектов известно, входит он во множество или нет. Множество может быть задано либо перечислением его элементов, либо описанием свойств его элементов. Символическая запись 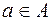 означает принадлежность элемента
означает принадлежность элемента 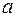 множеству
множеству  . Запись
. Запись 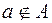 означает, что элемент
означает, что элемент 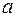 не принадлежит множеству
не принадлежит множеству  .
.
Если множество состоит из конечного числа элементов, оно называется конечным. При этом число элементов множества может быть очень велико или вообще неизвестно. Множество может состоять также из бесконечного количества элементов, тогда оно называется бесконечным.
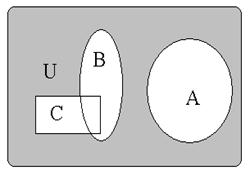
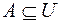 ; ; 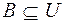 ; ;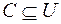 . .
| Множество  называют подмножеством другого множества называют подмножеством другого множества 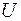 или множество или множество  включено в множество включено в множество 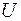 , если каждый элемент множества , если каждый элемент множества  является одновременно элементом множества является одновременно элементом множества 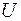 . Это обозначается . Это обозначается 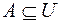 . Выделение подмножеств из множеств можно провести по различным признакам. В результате могут получиться как непересекающиеся подмножества (например, . Выделение подмножеств из множеств можно провести по различным признакам. В результате могут получиться как непересекающиеся подмножества (например,  и и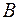 ), так и подмножества, имеющие общие элементы ( ), так и подмножества, имеющие общие элементы (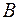 и и 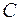 ). ).
|
Свойства включения:
1. Каждое множество есть подмножество самого себя 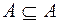 ;
;
2. Если 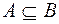 , а
, а 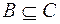 , то
, то 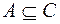 .
.
3. 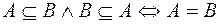 , т.е. множества
, т.е. множества  и
и 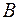 равны тогда и только тогда, когда эти множества состоят из одних и тех же элементов.
равны тогда и только тогда, когда эти множества состоят из одних и тех же элементов.
4. Каждый элемент множества  определяет некоторое подмножество множества
определяет некоторое подмножество множества  :
: 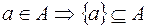
Множество, не содержащее ни одного элемента, называется пустым и обозначается 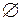 .
.
5. Любое множество содержит 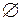 в качестве подмножества.
в качестве подмножества.
6. Каждое множество 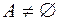 имеет по крайней мере два различных подмножества:
имеет по крайней мере два различных подмножества:  и
и 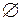 .
.
Множество  и
и 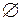 называют несобственными подмножествами множества
называют несобственными подмножествами множества  . Все остальные подмножества множества
. Все остальные подмножества множества  называются собственными или истинными. В этом случае, когда
называются собственными или истинными. В этом случае, когда 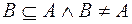 говорят, что
говорят, что 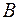 строго включено в
строго включено в  (обозначается
(обозначается 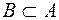 )
)
7. 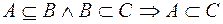
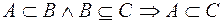
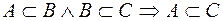
Множество всех подмножеств множества  называется множеством-степенью
называется множеством-степенью
P 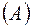 множества
множества  .
.
Если  не содержит элементов, т.е.
не содержит элементов, т.е. 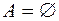 , то его единственным подмножеством является
, то его единственным подмножеством является 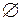 .
.
Если  – одноэлементное множество, т.е.
– одноэлементное множество, т.е. 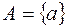 , то его подмножествами являются
, то его подмножествами являются  и
и 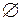 . Число этих подмножеств равно 2.
. Число этих подмножеств равно 2.
Если  – двухэлементное множество, т.е.
– двухэлементное множество, т.е. 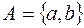 , то его подмножествами являются
, то его подмножествами являются 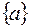 ,
, 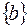 ,
,  и
и 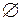 . Число этих подмножеств равно 4.
. Число этих подмножеств равно 4.
Несложно убедиться в том, что множество-степень P 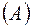 конечного
конечного 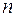 –элементного множества
–элементного множества 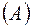 состоит из
состоит из 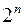 подмножеств.
подмножеств.
Основные операции над множествами
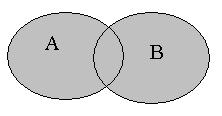
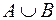
| Суммой или объединением двух или произвольного (даже бесконечного) числа заданных множеств называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из заданных множеств. Эта операция над множествами обозначается знаком 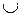 . .
|
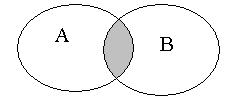
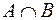
| Произведением или пересечением двух или произвольного (даже бесконечного) числа заданных множеств называется множество, состоящее из всех элементов, принадлежащих каждому из заданных множеств. Эта операция над множествами обозначается знаком 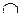 . Если . Если 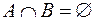 , то множества , то множества  и и 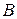 называются непересекающимися. называются непересекающимися.
|
Два множества называются непересекающимися (или расчлененными) если 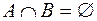 . Практический интерес представляют разбиения множества на взаимно непересекающиеся подмножества (эту задачу иногда называются классификацией). Разбиением множества
. Практический интерес представляют разбиения множества на взаимно непересекающиеся подмножества (эту задачу иногда называются классификацией). Разбиением множества  называется такая расчлененная система непустых подмножеств множества
называется такая расчлененная система непустых подмножеств множества  , что каждый элемент множества
, что каждый элемент множества  является элементом некоторого единственного множества этой системы. Возможность разбиения множества на непересекающиеся подмножества зависит от признака, по которому производится разбиение.
является элементом некоторого единственного множества этой системы. Возможность разбиения множества на непересекающиеся подмножества зависит от признака, по которому производится разбиение.
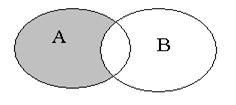
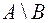
| Разностью множеств  и и 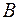 или дополнением или дополнением 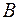 до до  называется множество, состоящее только из тех элементов называется множество, состоящее только из тех элементов  , которые не входят в , которые не входят в 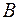 . Эта операция над множествами обозначается знаком . Эта операция над множествами обозначается знаком 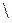 . .
|
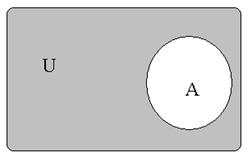
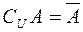
| Часто все рассматриваемые множества считают подмножествами одного основного множества 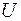 . В таком случае разность . В таком случае разность 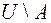 (дополнение (дополнение  до до 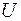 ) обозначают как ) обозначают как 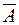 , а операцию называют взятием дополнения. , а операцию называют взятием дополнения.
|
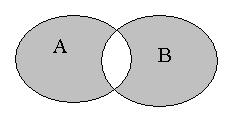
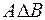
| Симметрической разностью множеств  и и 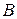 называется множество называется множество 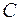 : :
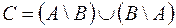 .
Обозначается симметрическая разность: .
Обозначается симметрическая разность: 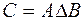 или или 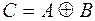 . .
|
Для подмножеств данного множества 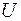 выполняются следующие законы:
выполняются следующие законы:
 Закон коммутативности (переместительный закон):
Закон коммутативности (переместительный закон):
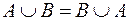 ;
; 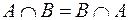 ;
;
 Закон ассоциативности (сочетательный закон) для любой тройки множеств
Закон ассоциативности (сочетательный закон) для любой тройки множеств  ,
, 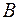 и
и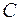 :
:
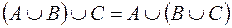 ;
;
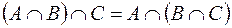 ;
;
 Закон дистрибутивности (распределительный закон) для любой тройки множеств
Закон дистрибутивности (распределительный закон) для любой тройки множеств 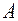 ,
, 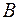 и
и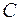 :
:
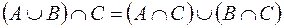 ;
;
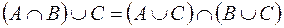 ;
;

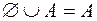 ;
; 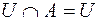 ;
;

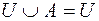 ;
; 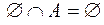 ;
;

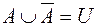 ;
; 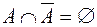 ;
;

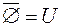 ;
;

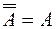 ;
;

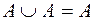 ;
;  ;
;

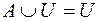 ;
; 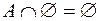 ;
;

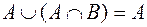 ;
; 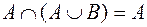 ;
;

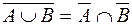 ;
; 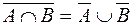 .
.
Если операции объединения множеств поставить в соответствие операцию сложения чисел, операции пересечения множеств – операцию умножения, универсальному множеству 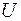 – единицу, а пустому множеству – ноль, то возникает аналогия между множествами и числами. Операции объединения и пересечения множеств, как и действия над действительными числами, подчиняются законам коммутативности, ассоциативности и дистрибутивности. Можно также провести аналогию между свойствами логических операций, где логической эквивалентности соответствует операция равенства, а операциям конъюнкции и дизъюнкции – операции объединения и пересечения.
– единицу, а пустому множеству – ноль, то возникает аналогия между множествами и числами. Операции объединения и пересечения множеств, как и действия над действительными числами, подчиняются законам коммутативности, ассоциативности и дистрибутивности. Можно также провести аналогию между свойствами логических операций, где логической эквивалентности соответствует операция равенства, а операциям конъюнкции и дизъюнкции – операции объединения и пересечения.
Свойства фигурируют попарно таким образом, что каждое получается из соседнего заменой 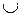 на
на 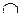 ,
, 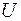 на
на 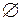 и наоборот. Такие выражения называются двойственными друг другу.
и наоборот. Такие выражения называются двойственными друг другу.
Принцип двойственности. Для любого тождества множеств двойственное ему выражение также является тождеством.
Очевидно, что операция разность не обладает свойствами коммутативности и ассоциативности, в то же время операция симметрическая разность и коммутативна, и ассоциативна.
Большое значение в современной математике имеет множественная операция декартово произведение. Если заданы два множества  и
и 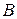 , то из их элементов можно составить упорядоченные пары, взяв сначала какой-либо элемент первого множества, а затем – элемент второго множества. Декартовым произведением двух исходных множеств
, то из их элементов можно составить упорядоченные пары, взяв сначала какой-либо элемент первого множества, а затем – элемент второго множества. Декартовым произведением двух исходных множеств  и
и 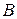 называется множество
называется множество 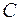 , составленное из упорядоченных пар (
, составленное из упорядоченных пар (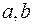 ). Декартово произведение множеств
). Декартово произведение множеств  и
и 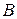 обозначается
обозначается 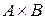 .
.
Очевидно, что 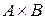 и
и 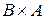 ‑ различные множества, т.е. операция декартова произведения не коммутативна, но, в то же время, она обладает свойством ассоциативности.
‑ различные множества, т.е. операция декартова произведения не коммутативна, но, в то же время, она обладает свойством ассоциативности.
|
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 507; Нарушение авторских прав?; Мы поможем в написании вашей работы!