Ранг матрицы. Рангом матрицы называется наибольший порядок ее миноров, отличных от нуля

Рангом матрицы называется наибольший порядок ее миноров, отличных от нуля. Ранг матрицы обозначают 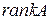или .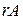

Если все миноры порядка 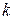данной матрицы равны нулю, то все миноры более высокого порядка данной матрицы также равны нулю. Это следует из определения определителя. Отсюда вытекает алгоритм нахождения ранга матрицы.

Если все миноры первого порядка (элементы матрицы ) равны нулю, то 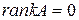. Если хотя бы один из миноров первого порядка отличен от нуля, а все миноры второго порядка равны нулю, то . Причем, достаточно просмотреть только те миноры второго порядка, которые окаймляют ненулевой минор первого порядка. Если найдется минор второго порядка отличный от нуля, исследуют миноры третьего порядка, окаймляющие ненулевой минор второго порядка. Так продолжают до тех пор, пока не придут к одному из двух случаев: либо все миноры порядка 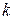, окаймляющие ненулевой минор 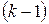-го порядка равны нулю, либо таких миноров нет. Тогда .

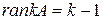Пример 10. Вычислить ранг матрицы .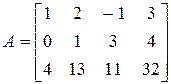

Минор первого порядка (элемент 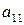) отличен от нуля. Окаймляющий его минор 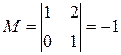тоже не равен нулю.

Далее рассмотрим миноры, окаймляющие минор :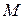

;

.

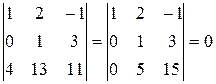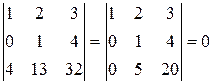Все эти миноры равны нулю, значит .

Приведенный алгоритм нахождения ранга матрицы не всегда удобен, поскольку связан с вычислением большого числа определителей. Наиболее удобно пользоваться при вычислении ранга матрицы элементарными преобразованиями, при помощи которых матрица приводится к столь простому виду, что очевидно, чему равен ее ранг.

Элементарными преобразованиями матрицы называют следующие преобразования:

Ø умножение какой-нибудь строки (столбца) матрица на число, отличное от нуля;

Ø прибавление к одной строке (столбцу) другой строки (столбца), умноженной на произвольное число.

Полужордановым преобразованием строк матрицы

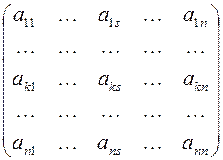
с разрешающим элементом 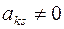называется следующая совокупность преобразований со строками матрицы:

Ø к первой строке прибавить ю, умноженную на число 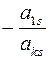и т.д.

Ø к последней строке прибавить ю, умноженную на число .

После выполнения этих преобразований получается матрица

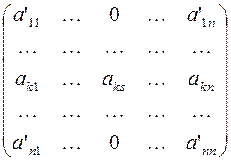
Полужордановым преобразованием столбцов матрицы с разрешающим элементом 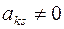называется следующая совокупность преобразований со столбцами матрицы:

Ø к первму столбцу прибавить й, умноженный на число 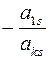и т.д.

Ø к последнему столбцу прибавить й, умноженный на число .

После выполнения этих преобразований получается матрица

Полужорданово преобразование строк или столбцов квадратной матрицы не изменяет ее определителя.

Элементарные преобразования матрицы не изменяют ее ранга. Покажем на пример, как вычислить ранг матрицы, пользуясь элементарными преобразованиями.

Пример 11. Вычислить ранг матрицы .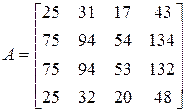

Применим к матрице элементарные преобразования: первую строку матрицы, умноженную на (-3) прибавим ко второй и третьей и ее же вычтем из последней.

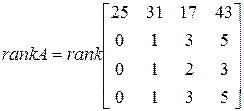
Вычитая далее вторую строку из третьей и последней, имеем:

.

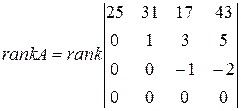Последняя матрица содержит отличный от нуля минор третьего порядка, определитель же самой матрицы равен нулю. Следовательно, .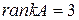

Отметим два важных свойства ранга матрицы.

Ранг матрицы не меняется при ее транспонировании.

Если ранг матрицы равен 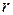, то любые ее 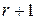строк (столбцов) линейно зависимы.

Обратная матрица

Пусть - квадратная матрица порядка 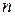. Матрица 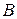называется обратной матицей к матрице , если выполняются равенства 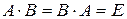, где ‑ единичная матрица порядка .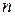

Теорема 1. Если для данной матрицы существует обратная матрица, то она единственная.

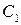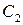Пусть и ‑ матрицы, обратные к матрице . Тогда 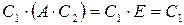, с другой стороны, .

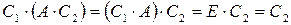Откуда . Обратную матрицу к матрице обозначают .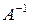

Теорема 2. Матрица имеет обратную матрицу тогда и только тогда, когда .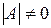

Пусть имеет обратную матрицу. Тогда 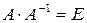и, применяя теорему об умножении определителей, получаем или 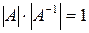. Следовательно, .

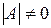Пусть 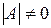. Укажем явное выражение матрицы 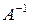через элементы матрицы , а именно: если , то

,

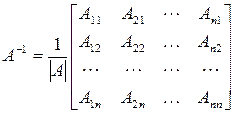(9.5)

здесь 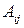‑ алгебраическое дополнение к элементу 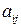. Матрица (9.5) получается из матрицы следующим образом. Сначала вместо каждого элемента 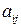пишется его алгебраическое дополнение, затем полученная матрица транспонируется и получается т.н. присоединенная матрица. Для получения обратной матрицы присоединенная матрица умножается на величину, обратную .

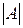Непосредственное умножение на матрицу (9.5) слева и справа дает единичную матрицу, что подтверждает, что (9.5) – матрица, обратная к .

Пример 12. Найти обратную матрицу к матрице .

Так как 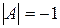, то 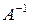существует. Вычислим алгебраические дополнения элементов матрицы :

,	,
,	,
,	,
,	,
.

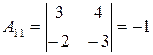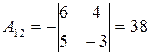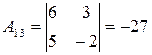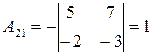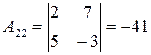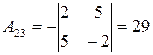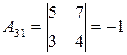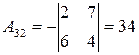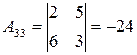Матрицу 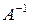находим в два приема, согласно формуле (9.5). Сначала запишем матрицу 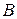, состоящую из алгебраических дополнений элементов . 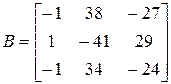Затем матрица 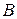транспонируется и умножается на число обратное 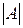, в данном случае – на (-1). Окончательно получаем:

.

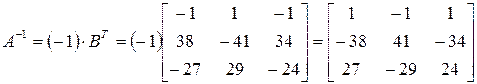Матрица называется неособенной или невырожденной, если ее определитель не равен нулю. Отметим свойства обратных матриц. Если и 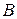‑ невырожденные матрицы одинакового порядка, то

,

,

,

.

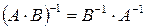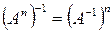Контрольные вопросы к теме

1. Понятие матрицы.

2. Виды матриц.

3. Понятие транспонирования матриц.

4. Операции сложения и вычитания матриц.

5. Операции умножения и возведения в степень матриц.

6. Понятие определителя.

7. Определитель - го порядка.

8. Правила нахождения определителей 2 и 3 порядка.

9. Свойства определителей.

10. Правила нахождения определителей - го порядка.

11. Понятие обратной матрицы.

12. Схема нахождения обратной матрицы.

13. Понятие ранга матрицы.

Лекция 10. *Понятие линейного оператора*

Основные понятия, включенные в систему тренинг- тестирования:

матрица перехода; линейное преобразование; собственное значение матрицы; собственный вектор матрицы; диагонализация матрицы; ортогональная матрица; характеристический многочлен.

Дата добавления: 2014-01-13