Канонический базис квадратичной формы

Лемма 2. Если – правильная рациональная дробь, а число (и – вещественные,) является корнем кратности многочлена, т.е. и, и если, то существуют вещественные числа и и многочлен с вещественными коэффициентами, такие, что где дробь также является правильной.

Лемма 1. Если – правильная рациональная дробь, а число является вещественным корнем кратности многочлена, т.е. и, то существует вещественное число и многочлен с вещественными коэффициентами, такие, что где дробь также является правильной.

При этом несложно показать, что полученное выражение является рациональной дробью с вещественными коэффициентами.

Рациональные дроби вида 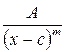, , 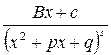, , ‑ трехчлен с действительными коэффициентами, не имеющий действительных корней, называются простейшими (или элементарными) дробями.

Всякая правильная рациональная дробь представима единственным образом в виде суммы простейших дробей.

При практическом получении такого разложения оказывается удобным так называемый метод неопределенных коэффициентов. Он состоит в следующем:

ü Для данной дроби пишется разложение, в котором коэффициенты считаются неизвестными ;

ü После этого обе части равенства приводятся к общему знаменателю и у получившихся в числителе многочленов приравниваются коэффициенты.

При этом если степень многочле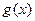на равна , то в числителе после приведения к общему знаменателю получается многочлен степени 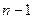, т.е. многочлен с 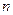коэффициентами.

Число неизвестных также равняется : .

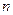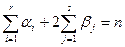Таким образом, получается система 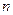уравнений с 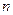неизвестными. Существование решения у этой системы следует из приведенной выше теоремы.

Контрольные вопросы к теме

1. Понятие многочлена.

2. Условие равенства многочленов.

3. Сложение и умножение многочленов.

4. Теорема о делении с остатком.

5. Понятие корня многочлена.

6. Понятие кратности корня многочлена

7. Теорема Безу.

8. Схема Горнера.

9. Соотношение степени многочлена и числа его корней.

10. Понятие правильной рациональной дроби.

11. Разложение правильной рациональной дроби на простейшие.

12. Метод неопределенных коэффициентов.

Лекция 12. *Квадратичные формы*

Основные понятия, включенные в систему тренинг-тестирования:

квадратичная форма; матрица квадратичной формы; канонический вид квадратичной формы; нормальный вид квадратичной формы; канонический базис квадратичной формы; канонический базис Якоби; угловые миноры матрицы квадратичной формы; положительно определенная квадратичная форма; отрицательно определенная квадратичная форма; критерий Сильвестра.

Понятие квадратичной формы.

Первоначально теория квадратичных форм использовалась для исследования кривых и поверхностей, задаваемых уравнением второго порядка, содержащими две или три переменные, Позднее эта теория нашла и другие приложения. В частности, при математическом моделировании экономических процессов целевые функции могут содержать квадратичные слагаемые. Многочисленные приложения квадратичных форм потребовали построения общей теории, когда число переменных равно любому 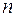, а коэффициенты квадратичной формы не всегда являются вещественными числами.

Квадратичной формой от 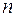неизвестных 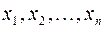называется сумма, каждое слагаемое которой является либо квадратом одного из неизвестных, либо произведением двух разных неизвестных.

Пример. Сумма 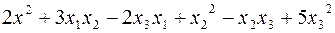является квадратичной формой от трех неизвестных .

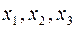Каждую квадратичную форму можно записать в стандартном виде. Для этого сначала приводятся подобные в квадратичной форме, затем коэффициенты при 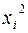обозначаются через 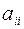, а коэффициенты при 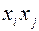через , причем Член 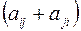записывается в виде . После этих преобразований квадратичную форму можно записать в виде:

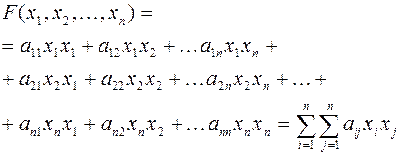
Матрица

называется матрицей квадратичной формы . Так как , то – симметричная матрица.

С учетом правила умножения матриц можно вывести матричную форму записи квадратичной формы.

,

где – матрица квадратичной формы,

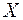– матрица–столбец неизвестных

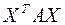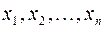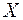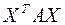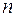Приведенные выкладки показывают, в частности, что если – симметрическая матрица, то выражение является квадратичной формой от неизвестных , т.е. квадратичная форма является результатом скалярного произведения матриц и . Матричная форма записи квадратичной формы имеет вид . Если – произвольный – мерный вектор, то после подстановки в квадратичную форму вместо 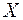получится число 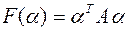, которое называется значением квадратичной формы на векторе .

Принято считать, что квадратичная форма имеет канонический вид, если все коэффициенты при произведениях различных переменных равны нулю, т.е. при 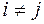. При этом квадратичная форма представляет собой сумму квадратов переменных с соответствующими коэффициентами 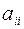, т.е.

.

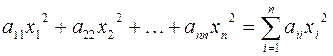В этом случае матрица квадратичной формы имеет диагональный вид:

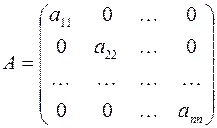
Очевидно, что изучение свойств квадратичной формы, записанной в каноническом виде, значительно упрощается. В связи с этим возникает задача приведения произвольной квадратичной формы к каноническому виду. В основе многих известных методов приведения квадратичной формы к каноническому виду лежит следующая теорема.

Дата добавления: 2014-01-13