
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Применение квадратичных форм к исследованию кривых второго прядка
|
|
|
|
Квадратичная форма отрицательно определена тогда и только тогда, когда главные миноры матрицы четного порядка положительны, а главные миноры матрицы нечетного порядка отрицательны.
Квадратичная форма положительно определена тогда и только тогда, когда главные миноры матрицы положительны.
Доказательство: Докажем первое утверждение.
Необходимость. Дано, что  положительно определена. Покажем, что все угловые миноры матрицы
положительно определена. Покажем, что все угловые миноры матрицы  отличны от нуля. Допустим обратное, и пусть
отличны от нуля. Допустим обратное, и пусть  . Тогда согласно Лемме найдется такой ненулевой вектор
. Тогда согласно Лемме найдется такой ненулевой вектор  , что
, что 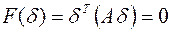 . Однако это противоречит положительной определенности квадратичной формы.
. Однако это противоречит положительной определенности квадратичной формы.
Итак, матрица  удовлетворяет условию Якоби, поэтому можно построить систему векторов Якоби
удовлетворяет условию Якоби, поэтому можно построить систему векторов Якоби  , которая является каноническим базисом
, которая является каноническим базисом  , причем выражение
, причем выражение 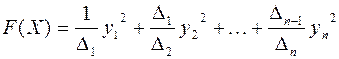 –
–
ее канонический вид в базисе  . Теперь из положительной определенности квадратичной формы и первого утверждения доказанной ранее теоремы следует, что
. Теперь из положительной определенности квадратичной формы и первого утверждения доказанной ранее теоремы следует, что 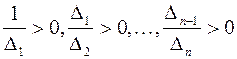 , и значит, что
, и значит, что 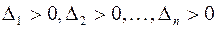 .
.
Достаточность. Если 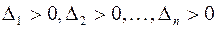 , то угловые миноры матрицы
, то угловые миноры матрицы  отличны от нуля и можно построить канонический базис квадратичной формы
отличны от нуля и можно построить канонический базис квадратичной формы  , в котором
, в котором 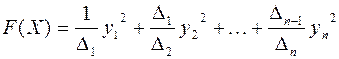 –
–
канонический вид квадратичной формы  . Поскольку
. Поскольку 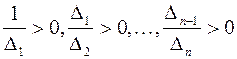 , то
, то  положительно определена.
положительно определена.
Аналогично доказывается второе утверждение теоремы.
В общем случае кривая второго порядка в базисе  описывается уравнением
описывается уравнением 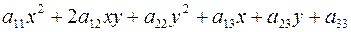 . Ее первые три слагаемые образуют квадратичную форму
. Ее первые три слагаемые образуют квадратичную форму  с матрицей
с матрицей
 .
.
Задача о приведении кривой 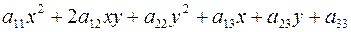 к каноническому виду сводится к задаче о приведении к каноническому виду квадратичной формы
к каноническому виду сводится к задаче о приведении к каноническому виду квадратичной формы  этой кривой.
этой кривой.
Пусть  и
и 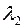 – собственные значения матрицы
– собственные значения матрицы  , а
, а  и
и  – ортонормированные собственные векторы матрицы
– ортонормированные собственные векторы матрицы  , соответствующие собственным значениям
, соответствующие собственным значениям  и
и 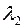 .
.
Ортонормированные векторы  и
и  называются главными направлениями этой кривой.
называются главными направлениями этой кривой.
Пусть  является матрицей перехода от ортонормированного базиса
является матрицей перехода от ортонормированного базиса  к ортонормированному базису
к ортонормированному базису 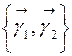 .
.
Тогда ортогональное преобразование

приводит квадратичную форму  к каноническому виду
к каноническому виду  , а уравнение кривой – к виду
, а уравнение кривой – к виду 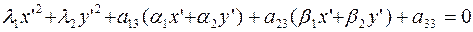 в прямоугольной декартовой системе координат
в прямоугольной декартовой системе координат 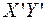 , оси которой направлены вдоль векторов
, оси которой направлены вдоль векторов  , а начало совпадает с точкой
, а начало совпадает с точкой 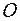 системы координат
системы координат  .
.
Выделив в этом уравнении полные квадраты, получим 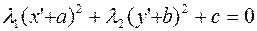 , где
, где 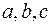 – некоторые числа. Осуществив параллельный перенос системы координат
– некоторые числа. Осуществив параллельный перенос системы координат 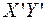 в новое начало
в новое начало  , получим канонический вид уравнения
, получим канонический вид уравнения  в системе координат
в системе координат  . В зависимости от чисел
. В зависимости от чисел 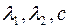 эта кривая будет эллипсом, гиперболой, параболой, парой прямых, точкой или мнимой кривой.
эта кривая будет эллипсом, гиперболой, параболой, парой прямых, точкой или мнимой кривой.
Контрольные вопросы к теме
1. Понятие квадратичной формы.
2. Построение матрицы квадратичной формы.
3. Канонический и нормальный вид квадратичной формы.
4. Канонический базис квадратичной формы и приведение квадратичной формы к каноническому виду.
5. Канонический базис Якоби.
6. Критерий Сильвестра знакоопределенности квадратичной формы.
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 680; Нарушение авторских прав?; Мы поможем в написании вашей работы!