И неравенства соответствует единственное решение неравенства

И неравенства, и, наоборот, каждому решению уравнения

Соответствует единственное решение уравнения

Теорема. Каждому решению неравенства

.

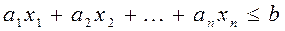
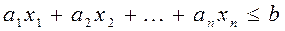Доказательство. Пусть – решение неравенства 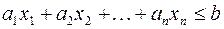. Тогда

или

Если в уравнение вместо переменных подставить значения =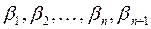, получится

Таким образом, решение 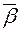удовлетворяет уравнению

и неравенству 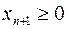. Доказана первая часть теоремы.

Пусть 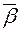удовлетворяет уравнению и неравенству 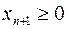, т.е. 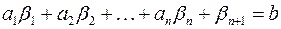и 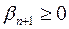. Отбрасывая в левой части равенства неотрицательную величину , получим

т.е. удовлетворяет неравенству

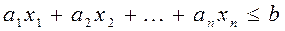
что и требовалось доказать.

Если в левую часть неравенств системы ограничений вида , добавить переменную , , то получится система ограничений – уравнений , . В случае, если система неравенств–ограничений имеет вид 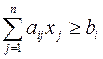, , то из левой части неравенств–ограничений нужно вычесть соответствующую неотрицательную дополнительную переменную , .

Полученная таким образом система уравнений–ограничений, вместе с условиями неотрицательности переменных, т.е. , и целевой функцией является канонической формой записи задачи линейного программирования.

Дополнительные переменные вводятся в целевую функцию с нулевыми коэффициентами и поэтому не влияют на ее значения.

В реальных практических задачах дополнительные неизвестные имеют определенный смысл. Например, если левая часть ограничений задачи отражает расход ресурсов на производство продукции в объемах , , а правые части - наличие производственных ресурсов, то числовые значения дополнительных неизвестных , означают объем неиспользованных ресурсов 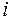-го вида.

Иногда возникает также необходимость перейти в задаче от нахождения минимума к нахождению максимума или наоборот. Для этого достаточно изменить знаки всех коэффициентов целевой функции на противоположные, а в остальном задачу оставить без изменения. Оптимальные решения полученных таким образом задач на максимум и минимум совпадают, а значения целевых функций при оптимальных решениях отличаются только знаком.

Дата добавления: 2014-01-13