Монотонность функции

Основные понятия

Тема 3. Исследование функций

Основные понятия, включенные в систему тренинг-тестирования:

монотонность функции; экстремум функции; локальный экстремум функции; стационарные точки функции; глобальный экстремум функции; выпуклость функции; точка перегиба функции; интерполяция функции; узлы интерполирования; интерполяционный полином Лагранжа; аппроксимация функций; формула Тейлора; формула Маклорена; эмпирические формулы; невязка.

Процесс управления требует от менеджера компактного представления разносторонних знаний из разных областей хозяйственной, управленческой, налоговой, коммерческой и других видов деятельности в виде разнообразных функциональных зависимостей.

В процессе такой деятельности перед менеджером возникают задачи тактического и стратегического планирования, оценки возможностей предприятия и конкурентов, оптимального распределения ресурсов, разумного реагирования на налоговую политику, выбора ценовой и инвестиционной политики и др.

Важную роль при этом играет исследование функций, используемых при построении математической модели рассматриваемой проблемы. Такое исследование проводится с учетом свойств конкретных функций и позволяет уточнить сформулированную математическую задачу, решая которую (с учетом выбранного метода решения), рассчитывают получить определенный результат, требующий в дальнейшем интерпретации в терминах исследуемой проблемы.

Все это связано с выявлением таких свойств функций, используемых в модели, как характер изменения (монотонность), наличие точек с особыми свойствами (стационарные точки, экстремумы), геометрические свойства (выпуклость графика функции) и другие.

Настоящий раздел посвящен исследованию функций методами дифференциального исчисления и использованию полученных навыков для решения задач.

Функция 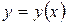называется возрастающей на промежутке , если 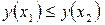для любых точек 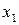и 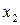из промежутка 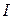, удовлетворяющих неравенству 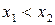. Функция называется убывающей на 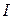, если из условия 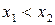следует .

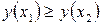Теорема. Если функция 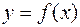непрерывна на отрезке 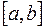, дифференцируема на интервале 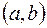, то для того, чтобы была возрастающей (убывающей) необходимо и достаточно, чтобы 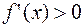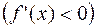в каждой внутренней точке интервала .

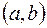Дифференцируемая функция является возрастающей на промежутке 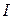тогда и только тогда, когда .

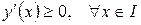Пример. Найти промежутки возрастания и убывания функции .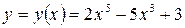

Вычислим : .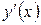

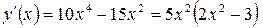Точки 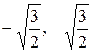делят числовую прямую на три интервала: .

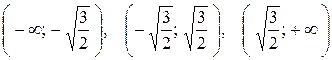Производная 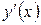положительна на интервалах 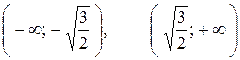. Следовательно, функция 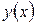возрастает на каждом из этих интервалов. На интервале 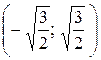производная 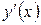неположительна, значит, 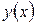убывает на этом интервале.

Дата добавления: 2014-01-13