Занятие 15

Практическое занятие по лекции №7

Занятие 14

Лекция № 8 Виды измерений. Классификация средств измерений. Определение точности измерений. Понятие погрешности измерения. Виды погрешностей. Показатели качества измерений и испытаний.

Виды измерений

В метрологии существует множество видов измерений, и число их постоянно увеличивается (рис. 14).

Измерения различают по способу получения информации, характеру изменений измеряемой величины в процессе измерений, количеству измерительной информации, отношению к основным единицам.

По способу получения информации измерения разделяют на прямые, косвенные, совокупные и совместные.

Прямые измерения – наиболее простые, состоящие в непосредственном сравнении физической величины с ее мерой. Например, при определении длины предмета линейкой происходит сравнение искомой величины (количественного выражения значения длины) с мерой, т.е. линейкой.

Косвенные измерения отличаются от прямых тем, что искомое значение величины устанавливают по результатам прямых измерении таких величин, которые связаны с искомой определенной известной зависимостью.

Например, объем параллелепипеда находят умножением трех линейных величин (длины, ширины и высоты); электрическое сопротивление – делением падения напряжения на силу электрического тока.

Совокупные измерения осуществляются одновременными прямыми измерениями нескольких одноименных величин, при которых искомое значение находят решением системы уравнений, составляемых в результате измерений различных сочетаний этих величин. При определении взаимоиндуктивности катушки, к примеру, используют два метода: сложения и вычитания полей.

Совместные измерения – это производимые одновременно (прямые и косвенные) измерения двух или более неодноименных физических величин для определения зависимости между ними.

Рис.14. Виды измерений

Совокупные и совместные измерения чаще всего применяют в измерениях различных параметров и характеристик в области электротехники.

Прямые измерения – основа более сложных измерений, поэтому целесообразно рассмотреть классификацию методов прямых измерений:

1. Метод непосредственной оценки, при котором величину определяют непосредственно по отсчетному устройству измерительного прибора, например измерение давления пружинным манометром, массы – на весах.

2. Метод сравнения с мерой, где измеряемую величину
сравнивают с величиной, воспроизводимой мерой. Например,
измерение массы на рычажных весах с уравновешиванием гирей;
измерение напряжения постоянного тока на компенсаторе сравнением
с ЭДС параллельного элемента.

3. Метод противопоставления, при котором измеряемая величина и
величина, воспроизводимая мерой, одновременно воздействуют на
прибор сравнения. Например, определение массы на равноплечих весах с помещением измеряемой массы и уравновешивающих ее гирь на двух чашках весов.

4. Дифференциальный метод, характеризуемый измерением
разности между измеряемой величиной и известной величиной,
воспроизводимой мерой. Метод позволяет получить результат
высокой точности при использовании относительно грубых средств
измерения.

5. Нулевой метод, который аналогичен дифференциальному, но в
нем разность между измеряемой величиной и мерой сводится к нулю.
При этом нулевой метод имеет то преимущество, что мера может
быть во много раз меньше измеряемой величины.

6. Метод замещения, состоящий в том, что измеряемую величину
замещают известной величиной, воспроизводимой мерой. Например,
взвешивание с поочередным помещением измеряемой массы и гирь
на одну и ту же чашку весов.

7. Метод совпадений, заключающийся в том, что разность между
сравниваемыми величинами измеряют, используя совпадение отметок
шкал или периодических сигналов. К примеру, при измерении длины
штангенциркулем наблюдают совпадение отметок на шкалах
штангенциркуля и нониуса; при измерении частоты вращения
стробоскопом наблюдают совпадение метки на вращающемся объекте
с момента вспышек известной частоты.

По характеру изменения измеряемой величины в процессе измерений бывают динамические и статические измерения.

Статистические измерения связаны с определением харак­теристик случайных процессов, звуковых сигналов, уровня шумов и т. д. Статические измерения имеют место тогда, когда измеряемая величина практически постоянна. Динамические измерения связаны с величинами, которые в процессе измерений претерпевают те или иные изменения. Статические и динамические измерения в идеальном виде на практике редки.

По количеству измерительной информации различают однократные и многократные измерения.

Однократные измерения – это одно измерение одной величины, то есть число измерений равно числу измеряемых величин. Практическое применение такого вида измерений всегда сопряжено с большими погрешностями, поэтому следует проводить не менее трех однократных измерений и находить конечный результат как среднее арифметическое значение.

Многократные измерения характеризуются превышением числа измерений над количеством измеряемых величин.

По способу определения значения измеряемой величины различают абсолютные и относительные измерения.

При абсолютном методе значение измеряемой величины определяется непосредственно по шкале прибора. При относительном – значение измеряемой величины получается как алгебраическая сумма показаний по шкале прибора и размера установочной меры, отклонение от которого показывает прибор.

Классификация средств измерений

Для практического измерения различных величин применяют технические средства, которые имеют нормированные метрологические характеристики, воспроизводящие и (или) хранящие единицу физической величины, размер которой принимают неизменным (в пределах установленной погрешности) в течение известного интервала времени, и называются средствами измерений (СИ). В метрологии средства измерения принято классифицировать по видам, метрологическому назначению и по принципам измерения.

Виды средств измерений

По видам все многообразие современных средств измерений разделяют следующим образом: меры, измерительные преобразователи, измерительные приборы, измерительные установки и системы, измерительные принадлежности.

Мерой называют средство измерений, предназначенное для воспроизведения и (или) хранения одного или нескольких заданных размеров физической величины, значения которых выражены в установленных единицах и известны с необходимой точностью.

К данному виду средств измерений относятся гири, концевые и угловые меры длины и т.п. На практике используют однозначные и многозначные меры, а также наборы и магазины мер. Однозначные меры воспроизводят величины только одного размера, многозначные меры воспроизводят несколько размеров физической величины. Например, линейка дает возможность выразить длину предмета в миллиметрах, сантиметрах и метрах.

К однозначным мерам относят и стандартные образцы, и стандартные вещества. Стандартный образец – это должным образом оформленная проба вещества (материала), которая подвергается метрологической аттестации с целью установления значения определенной характеристики. Эта характеристика (или свойство) является величиной с известным значением при установленных условиях внешней среды. К стандартным образцам относятся, например, наборы минералов с конкретными значениями твердости для определения этого параметра у различных минералов.

Наборы и магазины представляют собой объединение (сочетание) однозначных или многозначных мер для возможности воспроизведения некоторых промежуточных суммарных значений величины. Набор мер представляет комплект однородных мер разного размера, что дает возможность применять их в нужных сочетаниях, например набор плоскопараллельных концевых или угловых мер длины.

Магазин мер – сочетание мер, объединенных конструктивно в одно механическое целое, в котором предусмотрена возможность посредством ручных или автоматизированных переключателей, связанных с отсчетным устройством, соединять составляющие магазин меры в нужном сочетании. По этому принципу устроены магазины электрических сопротивлений.

При пользовании мерами следует учитывать номинальное и действительное значения меры, а также погрешность меры. Номинальным называют значение меры, указанное на ней. Действительное значение меры должно быть указано в специальном свидетельстве как результат высокоточного измерения с использованием официального эталона.

Разность между номинальным и действительным значениями называется погрешностью меры. Величина, противоположная по знаку погрешности, представляет собой поправку к указанному на мере номинальному значению. При аттестации (поверке) мер могут быть получены различные величины погрешности. Величина погрешности меры служит основой для разделения мер на классы, что обычно применимо к мерам, употребляемым для технических измерений.

Измерительный преобразователь – техническое средство, служащее для преобразования измеряемой величины в другую величину или измерительный сигнал, удобный для обработки, хранения и дальнейших преобразований, индикации и передачи.

Измерительные преобразователи либо входят в конструктивную схему измерительного прибора, либо применяются совместно с ним, но сигнал преобразователя не поддается непосредственному восприятию наблюдателем. Например, преобразователь может быть необходим для передачи информации в память компьютера. Преобразуемую величину называют исходной, а результат преобразования - выходной величиной. Основной метрологической характеристикой измерительного преобразователя считается соотношение между входной и выходной величиной, называемое функцией преобразования.

Измерительный прибор – средство измерений, предназначенное для получения значения измеряемой физической величины в установленном диапазоне. Это средство измерения, которое позволяет получать измерительную информацию в форме, удобной для восприятия пользователем. Различаются измерительные приборы прямого действия и приборы сравнения.

Приборы прямого действия отображают измеряемую величину на показывающем устройстве, имеющем соответствующую градуировку в единицах этой величины. Изменения рода физической величины при этом не происходит. К приборам прямого действия относят, например, микрометры, термометры и т.п.

Приборы сравнения предназначаются для сравнения измеряемых величин с величинами, значения которых известны. Такие приборы широко используются в научных целях, а на практике для измерения таких величин, как яркость источников излучения, давление сжатого воздуха и других.

Измерительные установки и системы – совокупности функционально объединенных мер, измерительных приборов, измерительных преобразователей и других измерительных устройств, предназначенные для измерения одной или нескольких физических величин и расположенные в одном месте. Обычно они автоматизированы и обеспечивают ввод информации в систему, автоматизацию самого процесса измерения, обработку и отображение результатов измерений для лучшего их восприятия.

Измерительные принадлежности – это вспомогательные средства измерений величин. Они необходимы для вычисления поправок к результатам измерений, если требуется высокая степень точности. Например, термометр может быть вспомогательным средством, если показания прибора достоверны только при строго регламентированной температуре; психрометр – если строго оговаривается влажность окружающей среды.

Следует учитывать, что измерительные принадлежности вносят в результат измерений определенные погрешности, связанные с погрешностью самого вспомогательного средства.

Метрологические назначения средств измерений

По метрологическому назначению средства измерений делят на два вида – рабочие средства измерений (РСИ) и эталоны.

Рабочие средства измерений применяют для определения параметров (характеристик) технических устройств, технологических процессов, окружающей среды и так далее. Рабочие средства могут быть лабораторными (для научных исследований), производственными (для обеспечения и контроля заданных характеристик технологических процессов), полевыми (для самолетов, автомобилей, судов и т.п.).

Каждый из этих видов рабочих средств отличается особыми показателями. Лабораторные средства измерений – самые точные и чувствительные, а их показания характеризуются высокой стабильностью. Производственные обладают повышенной устойчивостью к воздействиям различных факторов производственного процесса: температуры, влажности, вибрации и т.п. Полевые средства измерения могут работать в условиях изменяющихся в широких пределах внешних воздействий.

Особым средством измерений является эталон.

Эталон – это высокоточная мера, предназначенная для воспроизведения и хранения единицы величины с целью передачи ее размера другим средствам измерений. От эталонов единица величины передается рабочим средствам измерений.

Эталоны классифицируют на первичные, вторичные и рабочие.

Первичный эталон – это эталон, воспроизводящий единицу физической величины с наивысшей точностью, возможной в данной области измерений на современном уровне научно-технических достижений. Первичный эталон может быть национальным (государственным) и международным.

Национальный эталон утверждается в качестве исходного средства измерения для страны национальным органом по метрологии. В России национальные (государственные) эталоны утверждает Госстандарт РФ.

Первичному эталону соподчинены вторичные и рабочие (разрядные) эталоны. Размер воспроизводимой единицы вторичным эталоном сличается с государственным эталоном. Вторичные эталоны (их иногда называют «эталоны-копии») утверждают либо Госстандарт РФ, либо государственные научные метрологические центры, что связано с особенностями их использования. Рабочие эталоны (1-го, 2-го, 3-го разрядов) воспринимают размер единицы от вторичных эталонов и служат для передачи размера рабочим средствам измерений.

Принципы действия средств измерения

Это физические принципы (явления или совокупность явлений), положенные в основу построения средств измерения данного вида. Принцип действия обычно находит отражение в названии средства измерения. Количество принципов действия чрезвычайно велико и непрерывно увеличивается по мере использования для измерений новых физических явлений и их сочетаний.

Метрологические характеристики средств измерения

Метрологические характеристики – это характеристики, которые позволяют судить о пригодности средства измерения к измерениям в определенном диапазоне с определенной точностью. Средства измерения, имеющие метрологические характеристики, называются приборами, не имеющие – индикаторами.

Перечень метрологических характеристик, способы их нормирования и формы представления устанавливает ГОСТ 8.009-84.

Метрологические характеристики необходимы для достижения взаимозаменяемости средств измерения, сравнения средств измерения между собой и выбора требуемого по точности, оценки технического состояния средства измерения при поверке (калибровке), оценки погрешности измерения.

Наиболее распространены следующие метрологические характеристики.

Диапазон измерений средства измерений – область значений измеряемой величины, в пределах которой нормированы допускаемые пределы погрешности средства измерения.

Диапазон показаний средства измерений – область значений шкалы средства измерения, ограниченная начальным и конечным значениями шкалы.

Цена деления шкалы – разность значений измеряемой величины, соответствующих двум соседним отметкам шкалы средства измерения.

Погрешность средства измерения – разность между показаниями средства измерения и истинным (действительным) значением измеряемой физической величины. При проведении измерений используют т.н. допускаемую погрешность средства измерения, получаемую методами теории вероятности. В качестве предела допускаемой погрешности средства измерения принимают наибольшую погрешность, при которой средство измерения может быть допущено к применению. В этом качестве используют величину ± 3σ.

В зависимости от внешних условий погрешности средства измерения делятся на основные и дополнительные.

Основная погрешность средства измерения – это погрешность средства измерения, применяемого в нормальных условиях.

Нормальные условия измерений – условия измерений, характеризуемые совокупностью значений или областей значений влияющих величин, при которых изменениями результатов измерений пренебрегают вследствие малости. Для различных измеряемых величин нормальные условия задаются соответствующими нормативными документами.

Дополнительная погрешность средства измерен ия – составляющая погрешности средства измерений, возникающая дополнительно к основной погрешности вследствие отклонения какой-либо из влияющих величин от нормального ее значения или вследствие ее выхода за пределы нормальной области значений.

Рабочие условия измерений – условия измерений, при которых значения влияющих величин находятся в пределах рабочих областей.

В процессе эксплуатации метрологические характеристики средства измерения изменяются, что связано с процессами старения материалов и изнашиванием деталей его конструкции. Эти изменения приводят к отказам, т.е. невозможности средства измерения выполнять свои функции. Такие отказы называются метрологическими, т.к. они связаны с выходом метрологических характеристик из установленных пределов допускаемой погрешности.

Метрологическая исправность средства измерения – это состояние средства измерения, при котором всенормируемыеметрологические характеристики соответствуют установленным требованиям.

Метрологическая надежность средства измерения – это способность средства измерения сохранять свою метрологическую исправность в течение заданного времени при определенных режимах эксплуатации.

Метрологические характеристики средств измерения изменяются постепенно, что позволяет говорить о большом числе работоспособных состояний с различной степенью их приближения к допускаемым предельным значениям. В этом отличие метрологической надежности от общей теории надежности, в которой рассматриваются только два состояния системы: работоспособное и неработоспособное. Таким образом, метрологические характеристики средств измерения являются переменными (текущими) характеристиками, обладающими различными значениями в различные временные моменты.

Основной формой поддержания средства измерения в метрологически исправном состоянии является его периодическая поверка (калибровка).

Поверка (калибровка) средств измерений

Метрологическая надежность средств измерения обеспечивается путем их периодической поверки, которая осуществляется соответственно либо государственной метрологической службой (ГМС), либо метрологическими службами предприятий или ведомств.

Поверка средств измерений – это совокупность операций, выполняемых с целью определения и подтверждения действительных значений метрологических характеристик и пригодности к применению средств измерений. Под пригодностью средства измерения подразумевается соответствие его метрологических характеристик ранее установленным техническим требованиям, которые содержаться в технической документации на СИ (паспорте, аттестате), нормативных документах или определяются заказчиком.

В отличие от поверки, которую осуществляют органы государственной метрологической службы, калибровка может проводиться метрологической службой любого юридического лица или физическим лицом при наличии надлежащих требований к ним для выполнения этой работы. Калибровка заменила ранее существовавшую в нашей стране вневедомственную поверку и метрологическую аттестацию средств измерений. Кроме того, калибровка - добровольная операция, это еще одно ее отличие от поверки, которая обязательна через определенные межповерочные интервалы и осуществляется органами ГМС.

Однако добровольный характер калибровки не освобождает метрологическую службу предприятия от необходимости соблюдать определенные требования. Главное из них - обязательная "привязка" рабочего средства измерений к национальному (государственному) эталону через систему разрядных эталонов.

Сущность поверки (калибровки) рабочих средств измерений состоит в определении того, насколько хорошо передан размер единицы физической величины от эталонного к рабочему средству измерения. Эти технические процедуры осуществляются с помощью государственных эталонов и эталонов 1-го, 2-го, 3-го разрядов только при нормальных условиях.

Узловым вопросом при поверке является выбор соотношения между допустимыми погрешностями эталона и рабочего средства измерений. Обычно это соотношение 1:3 или 1:5. Очень важным при этом является соотношение диапазонов измерений эталона и рабочего средства измерений. Верхний предел измерений эталона должен быть равен или незначительно превышать верхний предел измерений рабочего средства измерений.

Для поверки рабочих измерительных устройств применяются следующие методы:

-непосредственное сличение рабочего средства измерений с эталонным измерительным устройством;

-прямое измерение рабочим средством измерений физической величины, воспроизводимой эталонной мерой.

Поверка средств измерений предполагает определение погрешностей средств измерения.

Как при поверке измерительного прибора методом прямого измерения величин, воспроизводимых мерами, так и при поверке методом непосредственного сличения с эталонным прибором наибольшую, полученную во всем диапазоне измерения погрешность принимают за основную погрешность поверяемого измерительного прибора. Основная погрешность средства измерения – это погрешность при использовании его в нормальных условиях.

При положительном исходе поверки средства измерений на него наносят поверочное клеймо – знак, удостоверяющий факт поверки и признания средства измерения пригодным к применению.

Определение точности измерений. Понятие погрешности измерения.

При практическом использовании тех или иных результатов измерений важно оценить их точность. Термин «точность измерений», т. е. степень приближения результатов измерения к некоторому истинному значению, не имеет строгого определения и используется для качественного сравнения измерительных операций. Для количественной оценки применяется понятие «погрешность измерений» (чем меньше погрешность, тем выше точность).

Погрешностью называют отклонение результата измерений от истинного (действительного) значения измеряемой величи­ны. При этом следует иметь в виду, что истинное значение физической величины считается неизвестным и применяется в теоретических исследованиях. Действительное значение физической величины устанавливается экспериментальным путем в предположении, что результат эксперимента (измерения) в максимальной степени приближается к истинному значению. Оценка погрешности измерения - одно из важных мероприятий по обеспечению единства измерений.

Погрешность измерений зависит в первую очередь от погрешностей СИ, а также от условий, в которых проводится измерение, от экспериментальной ошибки методики и субъективных особенностей человека в случаях, где он непосредственно участвует в измерениях. Поэтому можно говорить о нескольких составляющих погрешности измерений или о ее суммарной погрешности.

Количество факторов, влияющих на точность измерения, достаточно велико, и любая классификация погрешностей измерения (рис.15) в известной мере условна, так как различные погрешности в зависимости от условий измерительного процесса проявляются в разных группах.

Рис. 15. Классификация погрешностей измерения

Виды погрешностей

Как указывалось выше, погрешность измерения – это отклонение результата измерения Х от истинного Х_и значения измеряемой величины. При этом вместо истинного значения физической величины Х_и используют ее действительное значение Х_д.

В зависимости от формы выражения различают абсолютную, относительную и приведенную погрешности измерения.

Абсолютная погрешность – это погрешность средства измерений, выраженная в единицах измеряемой физической величины. Она определяется как разность Δ'= Х_i - Х_и или Δ = X - Х_д., где X_i – результат измерения.

Относительная погрешность – это погрешность средства измерений, выраженная отношением абсолютной погрешности средства измерений к результату измерений или действительному значению измеряемой физической величины. Она определяется как отношение δ = ±(Δ/Х_д)·100%.

Приведенная погрешность – это погрешность средства измерений, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений Χ_N.

В зависимости от характера проявления, причин возникновения и возможностей устранения различают систематическую и случайную погрешности измерений, а также грубые погрешности (промахи).

Систематическая погрешность – это составляющая погрешности, принимаемая за постоянную или закономерно изменяющуюся при повторных измерениях одного и того же параметра. Как правило, считают, что систематические погрешности могут быть обнаружены и исключены. Однако в реальных условиях полностью исключить эти погрешности невозможно. Всегда остаются какие-то неисключенные остатки, которые нужно учитывать, чтобы оценить их границы. Это и будет систематическая погрешность измерения.

Случайная погрешность – это составляющая погрешности, изменяющаяся в тех же условиях измерения случайным образом. Значение случайной погрешности заранее неизвестно, она возникает из-за множества не уточненных факторов. Исключить из результатов случайные погрешности нельзя, но их влияние может быть уменьшено путем статистической обработки результатов измерений.

Случайная и систематическая составляющие погрешности из­мерения проявляются одновременно, так что при их независимости их общая погрешность равна сумме погрешностей. В принципе систематическая погрешность тоже случайна и указанное деление обусловлено лишь установившимися традициями обработки и представления результатов измерения.

В отличие от случайной погрешности, выявляемой в целом, вне зависимости от ее источников, систематическая погрешность рассматривается по составляющим в зависимости от источников ее возникновения. Различают субъективную, методическую и инструментальную составляющие систематической погрешности.

Субъективная составляющая погрешности связана с индивидуальными особенностями оператора. Как правило, эта погрешность возникает из-за ошибок в отсчете показаний и неверных навыков оператора. В основном же систематическая погрешность возникает из-за методической и инструментальной составляющих.

Методическая составляющая погрешности обусловлена несовершенством метода измерения, приемами использования средств измерения, некорректностью расчетных формул и округления результатов.

Инструментальная составляющая возникает из-за собственно погрешности средств измерения, определяемой классом его точности, влиянием средств измерения на объект измерения и ограниченной разрешающей способности средств измерения.

Целесообразность разделения систематической погрешности на методическую и инструментальную составляющие объясняется следующим:

· для повышения точности измерений можно выделить лимитирующие факторы и, следовательно, принять решение либо об усовершенствовании методики, либо о выборе более точных средств измерения;

· появляется возможность определить составляющую общей погрешности, увеличивающейся либо со временем, либо под влиянием внешних факторов, и, следовательно, целенаправленно осуществлять периодические поверки и аттестации;

· инструментальная составляющая может быть оценена доразработки методики, а потенциальные точностные возможности выбранного метода определит только методическая составляющая.

Грубые погрешности (промахи) возникают из-за ошибочных действий оператора, неисправности средств измерения или резких изменений условий измерений. Как правило, грубые погрешности выявляются в результате статистической обработки результатов измерений при помощи специальных критериев.

Показатели качества измерений и испытаний

Единство измерений, однако, не может быть обеспечено только знанием погрешностей. При проведении измерений также важно знать показатели качества измерений. Под качеством измерений понимают совокупность свойств, обусловливающих получение результатов с требуемыми точностными характеристиками в необходимом виде и в установленные сроки.

Качество измерений характеризуется такими показателями, как точность, правильность и достоверность. Эти показатели должны определяться по оценкам, к которым предъявляются требования состоятельности, несмещенности и эффективности. Причем, в отличие от числовых характеристик, оценки являются случайными величинами, значение которых зависит от числа наблюдений n.

Состоятельной называют оценку, которая при n→ ∞ сводится по вероятности к оцениваемой величине.

Несмещенной называется оценка, математическое ожидание которой равно оцениваемой величине.

Эффективной называют такую оценку, которая имеет наименьшую дисперсию σ² = min.

Точность измерений определяется близостью к нулю погрешности результата измерения. Количественно точность может быть выражена обратной величиной модуля относительной погрешности, определенной в долях.

Правильность измерений определяется близостью к нулю систематической погрешности, т.е. результат «исправлен» на величину систематической погрешности.

Достоверность измерений определяется степенью доверия к результату и характеризуется вероятностью того, что истинное значение измеряемой величины лежит в указанных окрестностях действительного. Эти вероятности называют доверительными, а окрестности – доверительным интервалом с доверительными границами.

Доверительным интервалом от – Δ_д до + Δ_д называют интервал значений случайной погрешности, который с заданной доверительной вероятностью Р_д накрывает истинное значение измеряемой величины:

Р_д {`X - Δ<sub>д</sub> ≤ Х ≤ `X + Δ_д }.

При малом числе измерений (n 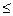20…25) и использовании нормального закона не представляется возможным определить доверительный интервал, так как нормальный закон распределения описывает поведение случайной погрешности в принципе при бесконечно большом числе измерений.

Поэтому при малом числе измерений используют распределение Стьюдента (предложенное английским статистиком Госсетом, публиковавшимся под псевдонимом «студент»), которое обеспечивает возможность определения доверительных интервалов при ограниченном числе измерений.

Границы доверительного интервала при этом определяются по формуле

Δ_д = t·S(),

где t – коэффициент распределения Стьюдента, зависящий от задаваемой доверительной вероятности Р_д и числа измерений n.

При увеличении числа наблюдений n распределение Стьюдента быстро приближается к нормальному распределению и совпадает с ним уже при n ≥30.

Следует отметить, что результаты измерений, не обладающие достоверностью, т. е. степенью уверенности в их правильности, не представляют ценности. К примеру, датчик измерительной схемы может иметь весьма высокие метрологические характеристики, но влияние погрешностей от его установки, внешних условий, методов регистрации и обработки сигналов приведет к большой конечной погрешности измерений.

При проведении испытаний их качество, наряду с такими показателями, как точность, правильность и достоверность, характеризуется также сходимостью и воспроизводимостью результатов.

Очевидно, что два испытания одного и того же объекта одинаковым методом не дают идентичных результатов. Объективной мерой их могут служить статистически обоснованные оценки ожидаемой близости результатов двух или более испытаний, полученных при строгом соблюдении их методики. В качестве таких статистических оценок согласованности результатов испы­таний и принимаются сходимость и воспроизводимость.

Сходимость – это близость результатов двух испытаний, полученных одним методом, на идентичных установках, в одной лаборатории.

Воспроизводимость отличается от сходимости тем, что оба результата должны быть получены в разных лабораториях.

Дата добавления: 2014-01-11