Проверка местной устойчивости элементов балки

Проверка местной устойчивости сжатого пояса не требуется, так как она была обеспечена надлежащим назначением отношения свеса пояса к толщине (см. п. 3.6.2).

Проверка местной устойчивости стенки балки. Под действием нормальных и касательных напряжений стенка балки может потерять местную устойчивость, т.е. может произойти ее местное выпучивание. Это произойдет в том случае, если действующие в балке отдельные виды напряжений или их совместное воздействие превысят критические напряжения потери устойчивости. Устойчивость стенки обычно обеспечивают не за счет увеличения ее толщины, что привело бы к повышенному перерасходу материала из-за большого размера стенки, а за счет укрепления ее ребрами жесткости.

Стенку балки следует укреплять поперечными ребрами жесткости, если значение условной гибкости 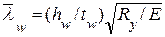превышает 3,2 при отсутствии местной нагрузки на пояс балки и 2,2 – при наличии местной нагрузки.

Определяем условную гибкость стенки:

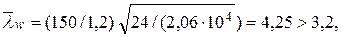
следовательно, поперечные ребра жесткости необходимы (рис. 3.14). Расстояние между основными поперечными ребрами a не должно превышать 2 h_w при l_w > 3,2 и 2,5 h_w при `l_w £ 3,2. Для балок, рассчитываемых в упругой стадии, допускается превышать указанные выше расстояния между ребрами до значения 3 h_w при условии передачи нагрузки через сплошной жесткий настил или при значении гибкости сжатого пояса балки λ_b = l_ef / b_f, не превышающем ее предельного значения λ_ub (в рассматриваемом примере это условие соблюдается: в середине пролета балки λ_b = 6,67< λ_ub = 15,64 и в измененном сечении λ_b = 12,56< λ_ub = 14,3), и при обязательном обеспечении местной устойчивости элементов балки.

Рис. 3.14. Схема балки, укрепленной поперечными ребрами жесткости

Расстояние между ребрами назначаем 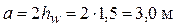, что увязывается с шагом балок настила 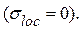При шаге а = 3 м поперечное ребро жесткости попадает на монтажный стык в середине пролета балки, поэтому первое и последующие за ним ребра смещаем к опоре на расстояние а /2 = 1,5м.

Ширина выступающей части парного ребра должна быть не менее

b_r = h_w /30 + 40 = 1500 / 30 + 40 = 90 мм.

для одностороннего – b_r = h_w /24 + 50 = 1500 / 24 + 50 = 112,5 мм.

Толщина ребра

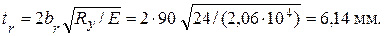
Принимаем ребро жесткости по ГОСТ 103–76* (табл. 3.7) из двух стальных полос 90´7 мм. Ребра жесткости привариваются к стенке непрерывными угловыми швами минимальной толщины. Торцы ребер должны иметь скосы с размерами не менее 40´40 мм для снижения концентрации сварочных напряжений в зоне пересечения сварных швов и пропуска поясных швов балки.

Поперечное ребро жесткости, расположенное в месте приложения сосредоточенной нагрузки F_b = 334,08 кН к верхнему поясу балки проверяют расчетом на устойчивость: двустороннее ребро – как центрально-сжатую стойку, одностороннее – как стойку, сжатую с эксцентриситетом, равным расстоянию от срединной плоскости стенки до центра тяжести расчетного сечения стойки. При этом в расчетное сечение стойки включают сечение ребра жесткости и устойчивые полосы стенки шириной

c = 0,65 t_w 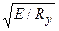= 0,65 · 1,2 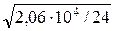= 22,85 см

с каждой стороны ребра, а расчетную длину принимают равной высоте стенки h_w = 1500 мм (рис. 3.15).

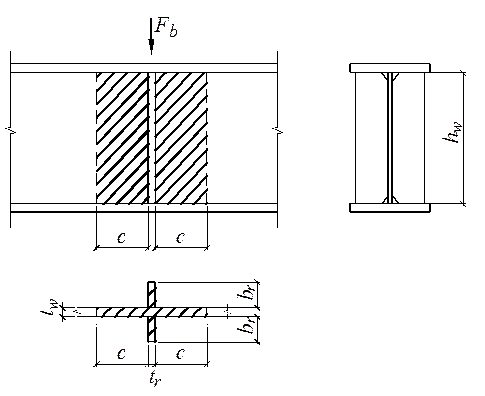
Рис. 3.15. Расчетное сечение условной стойки

Расчетная площадь стойки при двустороннем ребре

A_s = (2 b_r+ t_w) t_r+ 2 ct_w = (2 · 9 + 1,2) 0,7 + 2 ∙ 22,85 ∙ 1,2) = 68,28 см².

Момент инерции сечения стойки

I_z = t_r ³/12 + 2c t_w ³/12 = 0,7 (2 ∙ 9 +1,2)³ / 12 + 2 ∙ 22,85 ∙ 1,2³ / 12 = 412,88 см⁴.

Радиус инерции

i_z = 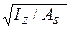= = 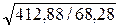2,46 см.

Гибкость стойки

λ_z = l_ef / i_z = 150 / 2,46 = 60,98.

Условная гибкость

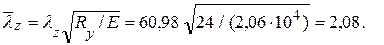
Производим проверку устойчивости стойки:

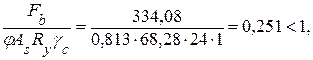
где φ = 0,813 – коэффициент устойчивости при центральном сжатии, принимаемый по табл. 3.11 в зависимости от условной гибкости λ_z для типа кривой устойчивости ^״ b ^״; тип кривой устойчивости зависит от формы сечений и толщины проката (табл. 3.12), при условной гибкости λ_z ≤ 0,4 коэффициент φ принимается равным единице.

Условие выполняется.

Таблица 3.11

Дата добавления: 2014-01-13