Предельные гибкости сжатых элементов

Стержней фермы

Определение расчетных длин и предельных гибкостей

В критическом состоянии потеря устойчивости при продольном изгибе сжатых стержней возможна в любом направлении (в плоскости фермы или из ее плоскости).

Предельная гибкость для сжатых элементов ферм и связей зависит от назначения стержня, степени его загруженности, оцениваемой коэффициентом

α = N /(φAR_yγ_c),

где N – расчетное усилие;

φAR_yγ_c – несущая способность стержня (табл. 5.2).

Таблица 5.2.

Элементы конструкций	Предельная гибкость λu
Пояса, опорные раскосы и стойки плоских ферм, передающие опорные реакции	180-60 α
Верхние пояса ферм, незакрепленные в процессе монтажа (предельную гибкость после завершения монтажа следует принимать по поз.1)
Основные колонны	180-60 α
Второстепенные колонны (стойки фахверка, фонарей и т.п.), элементы решетки колонн, элементы вертикальных связей между колоннами (ниже подкрановых балок)	210-60 α
Элементы связей, кроме указанных в поз. 4, а также стержни, служащие для уменьшения расчетной длины сжатых стержней, и другие ненагруженные элементы

Обозначение: 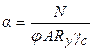– коэффициент, принимаемый не менее 0,5 (в необходимых случаях вместо φ следует применять φ_е).

Гибкие растянутые стержни могут провисать под действием собственного веса, легко повреждаться при транспортировании и монтаже, а при действии динамических нагрузок вибрировать, поэтому их гибкость тоже ограничена (табл. 5.3). При статических нагрузках гибкость растянутых элементов ограничивается только в вертикальной плоскости.

Гибкость стержня определяется его расчетной длиной l_еf (табл. 5.4) и радиусом инерции сечения i:

λ = l_еf / i.

Расчетные длины стержней определяются:

– в плоскости фермы

l_х = μl;

– из плоскости фермы

l_y = μl ₁,

где μ – коэффициент приведения длины к расчетной, зависящий от способов закрепления концов стержня;

l – геометрическая длина элемента (расстояние между центрами узлов);

l ₁ – расстояние между узлами, закрепленными от смещения из плоскости фермы (прогонами, специальными связями, жесткими плитами покрытий, прикрепленными к поясу сварными швами или болтами, и т.п.).

Таблица 5.3

Дата добавления: 2014-01-13