
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные свойства операций над множествами
|
|
|
|
Свойства операций над множествами
Операции над множествами, сформулированные в (1.4) обладают некоторыми свойствами, приведенными в табл. 1. Эти свойства выражаются совокупностью тождеств, справедливых независимо от конкретного содержания входящих в них множеств, являющихся подмножествами некоторого универсума U.
Таблица 1
1а) 
| 1б) 
|
2а) 
| 2б) 
|
3а) 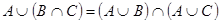
| 3б) 
|
4а) 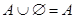
| 4б) 
|
5а) 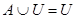
| 5б) 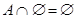
|
6а) 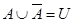
| 6б) 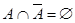
|
7а) 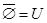
| 7б) 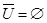
|
8а) 
| 8б) 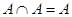
|
9а) 
| 9б) 
|
10а) 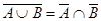
| 10б) 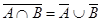
|
11) 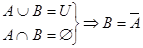
| |
12) 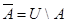
| |
13) 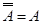 - закон двойного отрицания - закон двойного отрицания
| |
14) 
| |
15) 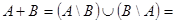 
| |
16) 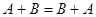
| |
| 17) (А + В) + С = А + (В + С) | |
| 18) А + Æ = Æ + А | |
19) =Æ =Æ
| |
20) 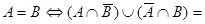 Æ Æ
|
Тождества (1а)-(3а) выражают соответственно коммутативный, ассоциативный и дистрибутивный законы для объединения, а тождества (1б)-(3б) - те же законы для пересечения. Соотношения (4а)-(7а) определяют свойства пустого множества Æ и универсума U относительно объединения, а соотношения (4б)-(7б) - относительно пересечения.
Выражения (8а) и (8б), называемые законами идемпотентности, позволяют записывать формулы с множествами без коэффициентов и показателей степени. Зависимости (9а) и (9б) представляют законы поглощения, а (10а) и (10б) - законы де Моргана.
Соотношения (11)-(20) отражают свойства дополнения, разности, дизъюнктивной суммы, включения и равенства.
Первые десять свойств в табл. 1 представлены парами двойственных (дуальных) соотношений, одно из которых получается заменой в другом символов: È на Ç и Ç на È, а также Æ на U и U на Æ. Соответствующие пары символов È, Ç и Æ, U называются двойственными (дуальными) символами.
При замене в любой теореме входящих в нее символов дуальными получим новое предложение, которое также является теоремой (принцип двойственности или дуальности). Тождество (11) не изменяется при замене символов дуальными, поэтому его называют самодвойственным.
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 384; Нарушение авторских прав?; Мы поможем в написании вашей работы!