Содержательный подход

Измерения информации

При определении количества информации рассматриваются два подхода:

1. Содержательный подход (количество информации как мера уменьшения неопределенности знаний) – рассматривает информацию с точки зрения ее содержания (новизны, понятности).

2. Объемный подход (алфавитный) к определению количества информации – рассматривает информацию с точки зрения хранения на физическом носителе и передаче с помощью технических средств (определяется объем информации).

За единицу измерения информации принимается 1 бит - такое количество информации, которое содержит сообщение, уменьшающее неопределенность знаний в два раза.

Что такое неопределенность знаний? Поясним на примере.

Допустим, вы бросаете монету, загадывая: орел или решка? Есть всего два возможных результата. Причем ни один из этих результатов не имеет преимущества перед другим, т.е. они равновероятны. Любой из вариантов ответа уменьшает неопределенность в 2 раза и, следовательно, количество информации равно 1 биту.

Количество информации (i), содержащееся в сообщении о том, что произошло одно из N равновесных событий, определяется из решения уравнения:

2^i=N

(1)

где: N – количество возможных результатов события

i – количество информации в сообщении об одном результате события (бит)

Формулу (1) назвали главной формулой информатики (учебник Семакина, Хеннера).

Прологарифмировав равенство (1) по основанию 2, получим: i*log₂2= log₂N, следовательно,

i = log2N

(2)

Задача.

Определить количество информации, полученное вторым игроком после первого хода первого игрока, в игре «крестики-нолики» на поле размером 8х8 клеток.

Решение. Перед первым ходом существует 64 возможных варианта расположения крестика: 64 = 2ⁱ , i =6. т.е. количество информации полученное вторым игроком после первого хода первого игрока составляет 6 битов.

Формула для вычисления количества информации для событий с различными вероятностями (например, если монета несимметрична (одна сторона тяжелее другой) - К.Шеннон (1948 год):

,

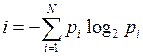где I – количество информации,

N – количество возможных событий,

p_i – вероятности отдельных событий

Чем меньше вероятности некоторого события (р), тем больше информации i содержит сообщение об этом событии:

i = log₂(1/p)

Задача. В непрозрачном мешочке хранится 10 белых, 20 красных, 30 синих и 40 зеленых шариков. Какое количество информации будет содержать зрительное сообщение о цвете вытянутого шарика?

Решение. Так как количество шариков различных цветов неодинаково, то вероятности зрительных сообщений о цвете вытянутого из мешочка шарика также различаются и равны количеству шариков данного цвета, деленному на общее количество шариков:

р_б = 10/100=0,1; р_к = 20/100=0,2; р_с = 30/100=0,3; р_з = 40/100=0,4

Применим формулу Шеннона для неравновероятных событий:

i = -(0,1*log₂0,1+0,2*log₂0,2+0,3*log₂0,3+0,4*log₂0,4) = 1,85 бита

Самостоятельно:

Задача 1. Группа школьников пришла в бассейн, в котором 4 дорожки для плаванья. Тренер сообщил. Что группа будет плавать на дорожке №3. Сколько информации получили школьники от этого сообщения? (Ответ – 2)

Задача 2. Сообщение о том, что ваш друг живет на 10 этаже несет 4 бита информации. Сколько этажей в доме? (Ответ – 16)

Дата добавления: 2014-01-13