Лекция № 16 Кооперативные игры в процессе Р УР

В матричной игре “2х3”.

Описание: Предприятие хочет купить три вида оборудования В1,В2 и В3 каждый вид по приемлемой для него цене А1, отличающейся от цены продавца А2, в соответствии со следующей исходной матрицей игры:

Предприятие	продавец		αi
В1	В2	В3
А1	О,7(a11)	0,4(a12)	0,5	0,4
А2	0,9(a21)	0,6(a22)	0,7	0,6
βj	0,9	0,6	0,7

Требуется найти такую ценовую стратегию предприятия, которая бы при заключении договора «купли – продажи» доставляла бы ему максимальную сходимость цен по всем трем видам оборудования.

При решении этой задачи седловая точка отсутствует, т.к. α ≠ β, но седловая точка присутствует по одному виду оборудования (В2=0,6). В этом случае задача может быть сведена к матричной игре «2х2». В противном случае решение игры следует искать в смешанных стратегиях для всех трёх видов продукции.

Кооперативные игры получаются в тех случаях, когда, в игре n игроков разрешается образовывать определённые коалиции. Обозначим через N множество всех игроков, N ={1, 2,..., n }, а через K – любое его подмножество. Пусть игроки из K договариваются между собой о совместных действиях и, таким образом, образуют одну коалицию. Очевидно, что число таких коалиций, состоящих из r игроков, равно числу сочетаний из n по r, то есть , а число всевозможных коалиций равно

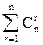= 2 ⁿ – 1.

Из этой формулы видно, что число всевозможных коалиций значительно растёт в зависимости от общего количества игроков в данной игре. Для исследования этих игр необходимо учитывать все возможные коалиции, и поэтому трудности исследований возрастают с ростом n. Образовав коалицию, множество игроков K действует как один игрок против остальных игроков, и выигрыш этой коалиции зависит от применяемых стратегий каждым из n игроков.

Функция u, ставящая в соответствие каждой коалиции K наибольший, уверенно получаемый его выигрыш u(K), называется характеристической функцией игры.

Так, например, для бескоалиционной игры n игроков u(K) может получиться, когда игроки из множества K оптимально действуют как один игрок против остальных NK игроков, образующих другую коалицию (второй игрок).

Характеристическая функция u называется простой, если она принимает только два значения: 0 и 1. Если характеристическая функция u простая, то коалиции K, для которых u(K)=1, называются выигрывающими, а коалиции K, для которых

u(K) = 0, – проигрывающими.

Если в простой характеристической функции u выигрывающими являются те и только те коалиции, которые содержат фиксированную непустую коалицию R, то характеристическая функция u, обозначаемая в этом случае через u _R,

называется - простейшей.

Содержательно простые характеристические функции возникают, например, в условиях голосования, когда коалиция является выигрывающей, если она собирает более половины голосов (простое большинство) или не менее двух третей голосов (квалифицированное большинство).

Более сложным является пример оценки результатов голосования в Совете безопасности ООН, где выигрывающими коалициями являются все коалиции, состоящие из всех пяти постоянных членов Совета плюс ещё хотя бы один непостоянный член, и только они.

Простейшая характеристическая функция появляется, когда в голосующем коллективе имеется некоторое “ядро”, голосующее с соблюдением правила “вето”, а голоса остальных участников оказываются несущественными.

Обозначим через u _G характеристическую функцию бескоалиционной игры. Эта функция обладает следующими свойствами:

1) персональность

u _G (Æ) = 0,

т.е. коалиция, не содержащая ни одного игрока, ничего не выигрывает;

2) супераддитивность

u _G (K È L) ³ u _G (K) + u _G (L), если K, L Ì N, K Ç L ¹ Æ,

т.е. общий выигрыш коалиции не меньше суммарного выигрыша всех участников коалиции;

3) дополнительность

u _G (K) + u(NK) = u(N) (16.1)

т.е. для бескоалиционной игры с постоянной суммой сумма выигрышей коалиции и остальных игроков должна равняться общей сумме выигрышей всех игроков.

Распределение выигрышей (делёж) игроков должно удовлетворять следующим естественным условиям: если обозначить через x_i выигрыш i- го игрока, то, во-первых, должно удовлетворяться условие индивидуальной рациональности

x_i ³ u(i), для i ÎN (16.2)

т.е. любой игрок должен получить выигрыш в коалиции не меньше, чем он получил бы, не участвуя в ней (в противном случае он не будет участвовать в коалиции);

во-вторых, должно удовлетворяться условие коллективной рациональности

= u(N) (16.3)

т.е. сумма выигрышей игроков должна соответствовать возможностям (если сумма выигрышей всех игроков меньше, чем u(N), то игрокам незачем вступать в коалицию; если же потребовать, чтобы сумма выигрышей была больше, чем u(N), то это значит, что игроки должны делить между собой сумму большую, чем у них есть). Таким образом, вектор

x = (x₁,..., x_n), удовлетворяющий условиям индивидуальной и коллективной рациональности, называется дележём в условиях характеристической функции u.

Система { N, u}, состоящая из множества игроков, характеристической функции над этим множеством и множеством дележей, удовлетворяющих соотношениям (16.2) и 16.(3) в условиях характеристической функции, называется классической кооперативной игрой.

Очевидно, в решение кооперативной игры должны входить дележи, лучшие с определён- ной точки зрения. Однако, найти делёж, который не только не доминировался бы какими-либо другими дележами, но сам доминировал бы любой другой делёж, не удаётся. Поэтому

решение отыскивают на пути расширения класса дележей. И это расширение состоит в том, что решением игры должен быть не один делёж, а некоторое их множество.

Дж. фон Нейман и О. Моргенштерн предложили потребовать от множества дележей, которое принимается в качестве решения кооперативной игры следующие два свойства:

- внутреннюю устойчивость, состоящую в том, чтобы дележи из решений нельзя было противопоставить друг другу;

- внешнюю устойчивость, состоящую в возможности каждому отклонению от решения противопоставлять некоторый делёж, принадлежащий решению.

В результате мы приходим к следующему определению.

Определение. Решением по Нейману-Моргенштерну (Н-М-решением) кооперативной игры называется множество R дележей в нём, обладающее следующими свойствами:

1) внутренняя устойчивость: никакие два дележа из R не доминируют друг друга;

2) внешняя устойчивость: каков бы ни был делёж S не принадлежащий R, найдётся делёж r, принадлежащий R, который доминировал бы S.

Содержательная интерпретация Н-М-решения состоит в том, что любые две нормы

поведения, соответствующие Н-М-решению, не могут быть противопоставлены друг другу; каково бы ни было отклонение от допустимых поведений, найдётся такая коалиция, которая будет стремиться к восстановлению нормы.

Свойство Н-М-решений.

Н-М-решение кооперативной игры не может состоять только из одного дележа, т.к. в этом случае характеристическая функция игры несуществует.

Дата добавления: 2014-01-13