При этом переменная определяется соотношениями

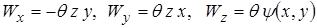, (2)

где - функция, определяющая депланацию поперечного сечения,

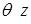- угол закручивания поперечного сечения на расстоянии от начала координат, - модуль упругости при сдвиге. - относительный угол закручивания.

Тогда компоненты напряжения определяются по формулам:

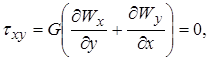
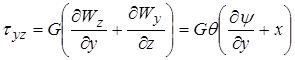(3)

Уравнения (1.1) и (1.2) в силу (3) удовлетворены автоматически. Если ввести функцию - функция напряжений, по формулам ; то (1.3) (4)

удовлетворяется. Тогда на (3)

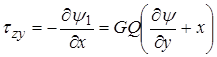(5)

Непосредственным дифференцированием можно показать, что удовлетворяет уравнению

. (6)

Если ввести 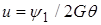, то (6)

если боковая поверхность стержня свободна от внешней нагрузки. При известном 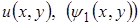все характеристики напряженно- деформированного состояния легко вычисляются.

Таким образом, определение напряженно-деформированного состояния при кручении прямолинейных стержней сводится к краевой задаче Дирихле для уравнения Пуассона. Задачу (7¢),(8¢) в общем виде представим в виде

Для решения уравнения Пуассона (задачи Дирихле) могут быть использованы различные методы, вариационные методы, методы операционного исчисления и Фурье, МКЭ, метод конечных разностей, метод конформных отображений и т.д.

Разностная схема решения задачи (7), (8)

Рассмотрим решение краевой задачи (7),(8)конечно- разностными методами. Для простоты решение (7),(8) рассмотрим в области

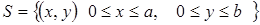- прямоугольник.

у

y_n=в

вh _у

h_x

ah_x

h _y

Область S заменяется сеточной областью:

;

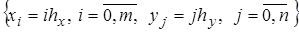Для аппроксимации производных используем пятиточечный трехслойный шаблон (шаблон типа «крест») и во внутренних узлах запишем центрально-разностные аппроксимации:

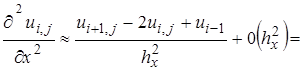
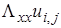(9.1)

i,j+1

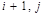
i-1,j i,j

i,j-1

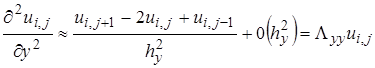(9.2)

Тогда конечно-разностный аналог для (7), (8) имеет вид:

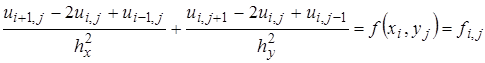; (10)

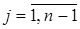; . (11)

Погрешность замены дифф. уравнением (7) есть 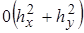. Уравнения (10) запишем в виде

(10¢)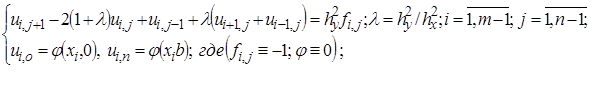

. (11¢)

Из задачи (10¢), (11¢) можно исключить граничные условия (11¢) путем внесения их в правую часть разностных уравнений (10¢): полагаем ;

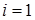Тогда с учетом уравнения (10¢) Þ:

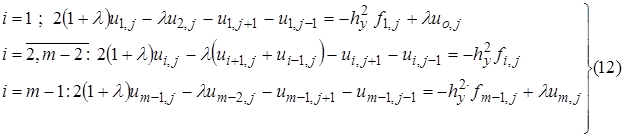где

Введем обозначения:

где

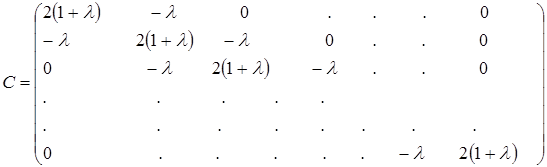(13)

Тогда :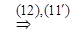

(14)

В нашем случае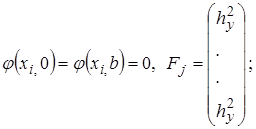

а) Систему (14) можно решить методом матричной прогонки (см. лаб. работу №3): .

б) Для решения системы уравнений (10¢), (11¢) может быть успешно использован итерационный метод Зейделя:

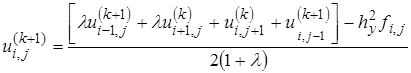; (15)

- номер итерации;

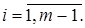
В качестве условия окончания итерационного процесса можно принять:

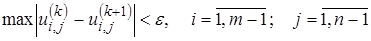. (16)

Здесь погрешность приближенного решения методом сеток задачи (7),(8) складывается из погрешности аппроксимации дифф. уравнения разностными и из погрешности, возникающей в результате приближенного решения системы разностных уравнений.

в) Метод установления

Для решения многих стационарных задач математической физики, описывающих равновесные состояния, рассматривают последние как результат установления развивающегося во времени процесса. Расчет новой нестационарной задачи часто оказывается проще, чем прямой расчет равновесного состояния (стационарной задачи).

Вместо стационарной задачи (7),(8):

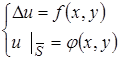вводится вспомогательная нестационарная задача

Поскольку функция и функция на границе не зависят от времени, то естественно ожидать, что решение с течением времени будет меняться все медленнее и нестационарное распределение

в пределе при 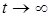превращается в стационарное решение 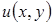задачи (7),(8). Поэтому вместо стационарной задачи (7),(8) можно решать нестационарную задачу (17),(18) до того времени 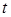, пока ее решение перестанет меняться в пределах интересующей нас точности, т.е. решение стационарной задачи (7),(8) находится как предел решения соответствующей нестационарной задачи (17),(18) при 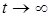. В этом состоит идея решения стационарных задач методом установления. Стремление пределу происходит с экспоненциальной скоростью =+.

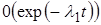Вместо разностной схемы (10),(11) рассмотрим три различные разностные схемы для задачи (17),(18):

1) простейшая явная разностная схема:

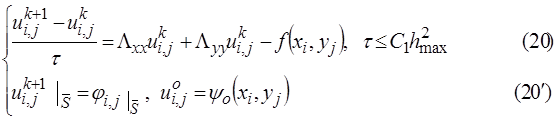
;для явных схем ; – номер слоя по времени.

2) Неявная схема

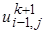
u

u

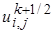
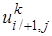
3) Схема переменных направлений

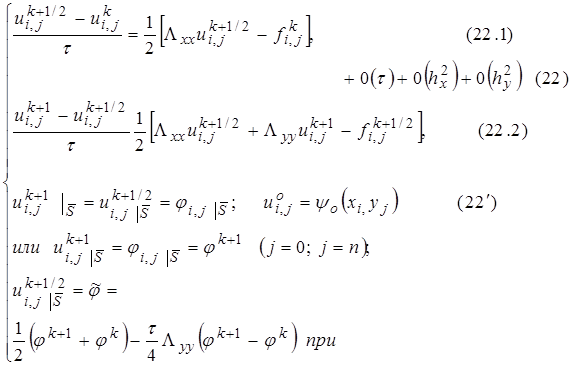
Будем считать, что на границе выполняется:

Здесь - означает временной шаг: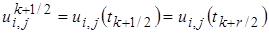

1)Вычислим по уже известному 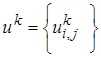для схемы (20), (20¢) осуществляется по явным формулам. Явная схема устойчива при ~;

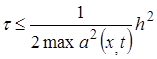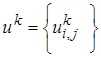2) Вычисление при уже вычисленном по схеме (21),(21¢) требует решения задачи

(21)

Эта задача ничем не проще исходной задачи (10),(11). Поэтому простейшую неявную схему не имеет смысла использовать для приближенного вычисления.

3) Вычисление по уже известным по схеме (220 осуществляется прогонками в направлении оси ОХ для вычисления 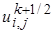одномерных задач при каждом фиксированном 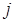, а затем прогонками в направлении оси ОУ для вычисления решений одномерных задач при каждом фиксированном . (Схема переменных направлений – Пислина-Рекфорда). Количество арифметических действий при этом пропорционально числу неизвестных (для уменьшения ошибки к раз число арифметических действий будет 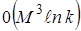, 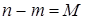. Уравнения (22.1), (22.2)представим в виде:

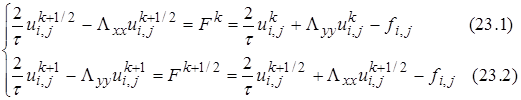(23)

или

(24.1)

при при .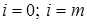

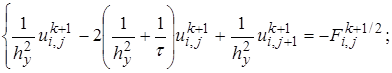(24.2)

при при .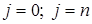

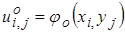
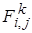Пусть задано . Тогда вычисляем . Затем методами прогонки (факторизации) вдоль строк решаем задачу (24.1) (при каждом фиксированном 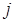) и определяется 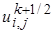во всех узлах сетки и после чего вычисляем 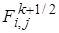и решаем задачу (24.2) вдоль столбцов (при каждом фиксированном ). Определяется . После этого при переходе от слоя к слою процедура счета повторяется, т.е. происходит все время чередование направлений. Схема переменных направлений является экономичной, абсолютно устойчивой.

Разностные схемы, в которых число арифметических действий для перехода от к пропорционально числу неизвестных значений, называемых экономичными (на узел сетки приходится число действий, не зависящее от количества узлов).

Счет по методу установления (схемы(24.1),(24.2)) проводится до тех пор, пока не выполняется условие

т.е. пока не получим стандартного решения (- перестает меняться во времени).

Разностная задача аппроксимирует исходную точную с порядком 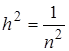. Поэтому точное решение отличается от приближенного (14) или (24) на величину порядка 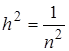. В связи с этим нет смысла вычислять решение с большей точностью. Добиваться уменьшения первоначальной погрешности более чем в Ораз было бы нецелесообразной затратой вычислительной работы. На практике, при решении конкретных задач, обычно ограничивается обоснованиями принципиального характера на модельных (тестовых) задачах. Конкретные суждения о погрешности получаются не из теоретических оценок, а из сравнения между собой результатов расчета, выполненных на сетках с различными значениями.

Дата добавления: 2014-01-13