Тепер множина оптимальності знайденого базису визначається системою нерівностей

2 / 7 + l3 / 7 ³ 0;

-4 / 7 + l / 7 ³ 0,

розв’язок якої - l ³ 4, базисні змінні - x₁, x₂, x₅, цільова функція визначається виразом F = 8 + l.

Розв’язування задачі параметричного програмування

з параметром у правих частинах обмежень

Загальний вигляд задачі:

F= (c,x) min, (13.5)

Ax = b (l), (13.6)

x ³ 0, (13.7)

де b(l) = b¹ + lb². Це означає, що b_i(l) = b_i¹ + l b_i², i = 1, m, m - кількість рядків матриці А _{m х n} обмежень.

Будемо вважати, що цільова функція задачі (13.5 – 13.7) обмежена, оскільки праві частини на цю властивість не впливають. Дійсно, нехай при поданій сукупності значень правих частин обмежень від поданої симплекс-таблиці за допомогою послідовності симплексних перетворень можна перейти до симплекс-таблиці зі стовпчиком з від’ємним коефіцієнтом у індексному рядку і усіма недодатніми коефіцієнтами обмежень. Тоді при будь-якій іншій поданій сукупності значень правих частин обмежень та ж сама послідовність симплексних перетворень утворює стовпчик, що свідчить про необмеженість цільової функції.

Покладемо l = l₀, і спробуємо знайти відповідний розв’язок отриманої задачі лінійного програмування. В результаті застосування симплекс-методу можливі два випадки:

1) при поданому l₀ знайдено оптимальний план;

2) при поданому l₀ обмеженння не сумісні.

Розглянемо перший випадок. В результаті застосування симплекс-методу права частина обмежень приймає вигляд

b^’(l₀) = B^-1~ b (l₀) = B^-1~ (b¹ + l₀ b²) = B^-1~b¹ + l₀ B^-1~ b² = b^1’+l₀b^2’.

Як бачимо, права частина обмежень лінійно залежить від l₀ :

b^’_i = b¹_i^’ + l₀ b²_i^’, i = 1,m.

Якщо при будь-якому поданому l усі праві частини невід’ємні, то отримана симплексна таблиця дає розв’язок для цього l. Тому множина оптимальності знайденого базису визначається системою нерівностей

b¹ _i^’ + l b²_i^’ ³ 0, i = 1,m.

Наслідком цієї системи є наступні співвідношення. Якщо b² _i^’ > 0, l ³ -b¹ _i^’ / b² _i^’. При b² _i^’ < 0, l £ - b¹ _i^’ / b² _i^’ .

Позначимо

max { - b¹ _i^’ / b² _i^’ }; min { - b¹ _i^’ / b² _i^’ };

l = i | b²_i^’ > 0 l = i | b²_i^’ < 0

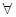
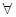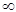- , b²_i^’ £ 0, i; 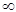, b²_i^’ ³ 0, i.

Очевидно, що знайдений для l₀ базис залишається оптимальним, якщо виконується умова l £ l £ l.

Тепер проаналізуємо задачу (13.5) – (13.7) при l ³ l. Будемо вважати, що l < 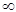, бо інакше знайдений базис залишається оптимальним при усіх l ³ l. Це означає, що серед коефіцієнтів b²_i^’ є принаймні один від’ємний. Нехай b²_r^’ < 0, і - b ¹ _r^’ / b ² _r^’ = l. Тоді b^’ _r (l) = b ¹ _r^’ + l b ² _r^’ = 0, і тому b^’ _r (l) = b ¹ _r^’ + l b ² _r^’ + (l - l) b ² _r^’ = (l - l) b ² _r^’.

У отриманій оптимальній симплекс-таблиці для r-го рядка виконується одна з двох умов: а) усі елементи a^’_rj (j = 1, n) невід’ємні; б) принаймні один з елементів (наприклад, a^’_{r k} ) менше нуля.

При виконанні умови а) для усіх l > l, враховуючи, що b ² _r^’ < 0, маємо b^’ _r (l) < 0, і це означає, що система обмежень не сумісна.

У випадку виконання умови б) згідно з двоїстим симплекс-методом виведемо з базису стовпець a^r’, якому відповідає базисна змінна r-го рядка, і уведемо у базис k-й стовпець a^k’. Для k -го стовпця виконується умова

c_k^’/ a_rk^’ = min {| c_j^’ / a_rj^’ |}.

j | a_rj^’ < 0

Покажемо, що отриманий новий базис є оптимальним принаймні для l = l. Згідно з формулою симплексного перетворення маємо

b^’’_i (l) = b^’_i (l) - (a_ik^’ / a_rk^’)b^’_r (l), i = 1,m.

При l = l b^’’_i (l) = b^’_i (l) ³ 0 (оскільки b^’_r (l) = 0), i = 1,m.

Знайдемо такі значення l, при яких

b^’’_i (l) = b^1’’_i + l b^2’’_i ³ 0, i = 1,m. (13.8)

При переході до нового базису b^1’_i і b^2’_i перетворюються за формулами

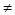
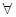b^1’’_i = b^1’_i - (a_ik^’ / a_rk^’)b^1’_r, b^2’’_i = b^2’_i - (a_ik^’ / a_rk^’)b^2’_r, i r,

і b^1’’_r = b^1’_r / a_rk^’, b^2’’_r = b^2’_r / a_rk^’ .

Для усіх l, що задовольняють умові (13.8), має місце нерівність

b^1’’_r + l b^2’’_r ³ 0.

Тому b^1’_r / a_rk^’ + l b^2’_r / a_rk^’ ³ 0, або, враховуючи, що a_rk^’ < 0, b^1’_r + l b^2’_r £ 0.

за припущенням b^2’_r < 0, тому l ³ - b^1’_r / b^2’_r = l. Отриманий результат можна сформулювати у вигляді теореми.

Теорема 13.2. (Про розв’язування задачі лінійного програмування з параметром у правій частині обмежень). Нехай l < 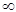, і індекс r визначається умовою

- b¹_r^’ / b²_r^’ = min{ - b¹_i^’ / b²_i^’ } = l.

i | b²_i^’ < 0

Тоді:

а) якщо a^’_rj ³ 0, j = 1,n, система обмежень для l > l не сумісна;

б) якщо деяке a_rk^’ < 0 і c_k^’ / a_rk^’ = min {| c_j^’ / a_rj^’ |}, то після уведення у

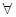a_rj^’ < 0

поточний базис стовпця a^k’ утворюється новий базис, нижня межа множини оптимальності якого співпадає з l.

Таким чином, процес дослідження параметричної задачі для l > l зводиться до просування за базисами її сусідніх планів. Причому права межа множини оптимальності попереднього базису є лівою межою для множини оптимальності наступного базису. Процес припиняється визначенням необмеженої справа області значень параметра l, що є або множиною оптимальності останнього базису, або множиною, у кожній точці якої система обмежень не сумісна.

Аналогічна ситуація має місце і при дослідженні задачі при l < l.

У випадку 2), коли при l = l₀ задача розв’язку не має (система обмежень не сумісна), отримуємо або область значень l, обжену з одного боку, і тоді можна перейти до сусіднього базису, або область, не обмежену з обох боків. І тоді задача не має розв’язку при жодному значенні l.

Розглянемо приклад розв’язування задачі з параметром у правих частинах обмежень.

F = x₁ - 2x₂ min;

2x₁ + x₂ ³ 6;

-x₁ +3x₂ £ 11;

3x₁ -2x₂ £ 2l;

x₁,x₂ ³ 0.

У поданому випадку b₁¹ = 6, b₁² = 0, b₂¹ = 11, b₂² = 0, b₃¹ = 0, b₃² = 2.

Таблиця 13.4

Пс.-баз. змінні	Праві част.	x1	x2	x3	x4	x5	x6
x3	-6	-2	-1
x4		-1
x5	2l		-2
x6	M
-F			-2
x3	M-6	-2
x4	11-3M	-1					-3
x5	2l +2M
x2	M
-F	2M
x3	-7/3	-7/3			1/3
x6	M-11/3	1/3			-1/3
x5	2l+22/3	7/3			2/3
x2	11/3	-1/3			1/3
-F	22/3	1/3			2/3
x1				-3/7	-1/7
x6	M-4			1/7	-2/7
x5	2l+5
x2				-1/7	2/7
-F				1/7	5/7

Застосування двоїстого симплекс-методу для пошуку оптимального базису ілюструється табл.13.4.

З останньої таблиці отримуємо, що базис, якому відповідають базисні змінні x₁, x₂, x₅, x₆, залишається оптимальним для усіх значень параметра, задовольняючих нерівності 2l + 5 ³ 0, або l ³-5/2. При цьому цільова функція зберігає стале значення, що дорівнює -7.

При l < -5/2 система обмежень несумісна, оскільки третій рядок у останній симплекс-таблиці не містить жодного від’ємного коефіцієнта.

Дата добавления: 2014-01-13