Рівняння з однією змінною

Тема: РІВНЯННЯ, ЇХ СИСТЕМИ І СУКУПНОСТІ

Нехай на множині М задано два вирази f (х) і q (x) з однією змінною х. Предикат виду f (х) = q(x), х Î М, для якого потрібно знайти область істинності, називається рівнянням з однією змінною. Вирази f (х) і q (x) називаються частинами рівняння, f (х) – лівою, q (x) – правою. У тому разі, коли хоч одна з частин рівняння є алгебраїчною сумою, доданки суми називаються членами рівняння. Множина М називається областю визначення рівняння.

Згідно з означенням рівняння з однією змінною є предикатом, а тому до нього можна застосувати всі ті поняття, які використовуються для характеристики предиката. Множина істинності предиката, що задає рівняння, називається множиною розв’язків рівняння (множиною коренів рівняння), а кожне число, яке належить цій множині, називається розв’язком (коренем) даного рівняння. Розв’язати дане рівняння – означає знайти множину його розв’язків.

Часто область визначення рівняння не вказується, в цьому разі її потрібно встановити: вона є перерізом областей визначення кожного з виразів f (х) і q (x) рівняння (кожної з частин рівняння). Залежно від області визначення рівняння може мати різні множини розв’язків. Наприклад, рівняння

(x – 1) (х + 2) (х² – 3)(x² + 1) = 0

на множині натуральних чисел має один розв’язок, бо тільки при х = 1 добуток множників дорівнює нулю, на множині цілих чисел – два розв’язки {–2; 1}, а на множині дійсних чисел – чотири розв’язки {–2; – 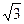; 1; }.

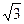Прийнято також не вказувати область визначення рівняння в тих випадках, коли вона дорівнює найширшій числовій множині, яка відома тому, хто розв’язує рівняння. Зокрема, у міру ознайомлення учнів з числовими множинами, такою множиною для молодших школярів є множина цілих невід’ємних чисел, а для учнів середньої школи – множина дійсних чисел.

Два рівняння з однією змінною, визначені на множині М, називаються рівносильними на ній, якщо їх множини розв’язків збігаються. Два рівняння, визначені на множині М, є рівносильними на ній і тоді, коли на цій множині вони розв’язків не мають.

З означення випливає, що рівносильність рівнянь істотно залежить від їх області визначення: зміна її може привести до порушення рівносильності. Наприклад, рівняння

(х – 1)(х + 3) = 0 і (х – 1)(х + 2) = 0,

рівносильні на множині натуральних чисел, бо вони мають на ній своїм розв’язком лише число 1, і нерівносильні на множні цілих чисел, бо на ній, крім одиниці, перше рівняння має розв’язком число – 3, а друге – число – 2.

Відношення рівносильності рівнянь є відношенням еквівалентності і задає на множинні рівнянь розбиття на класи рівносильних між собою рівнянь. Це дає змогу при розв’язуванні рівнянь заміняти їх на рівносильні, розв’язки яких легше знайти.

У процесі розв’язування над рівняннями здійснюються різні перетворення. Однак не всі з них приводять до одержання рівносильних рівнянь. Наприклад, заміна рівняння

(х – 1)(х – 3) = х – 3 (1)

рівнянням

х – 1 = 1 (2)

неправильна, бо рівняння нерівносильні на множині дійсних чисел. Справді, рівняння (1) має множину розв’язків {2, 3}, а (2) – { 2 }. Рівняння (2) одержане з рівняння (1) діленням обох частин на вираз х – 3, який дорівнює нулю при х = 3 і при цьому втрачаємо розв’язок х = 3 першого рівняння.

Якщо ж рівняння

Х – 1 = 2 (3)

замінити рівнянням

(х – 1)² = 4, (4)

то також одержимо нерівносильне йому рівняння, бо рівняння (3) має множину розв’язків {3}, а рівняння (4) – {–1; 3}, Отже, множини розв’язків не рівні, а тому, за означенням, рівняння нерівносильні на множині дійсних чисел. Розв’язок х = –1 буде стороннім для рівняння (3). З точки зору математичної логіки рівняння (4) є лише логічним наслідком рівняння (3).

Користуючись поняттями математичної логіки, можна дати означення рівносильності рівнянь з однією змінною по-іншому.

Два рівняння з однією змінною, визначені на множині М, називаються рівносильними на ній, якщо кожне з них є логічним наслідком другого.

Широке використання перетворень, що їх доводиться виконувати при розв’язуванні рівнянь, базується на застосуванні таких двох теорем.

Теорема 1. Якщо до обох частин рівняння з однією змінною, визначеного на множині М, додати вираз, визначений на цій же множині, то одержимо рівняння, рівносильне заданому на множині М.

Нехай

f (х) = q (x), х Î М, (1)

дане рівняння і j (х), х Î М, – вираз, який додаємо до обох частин рівняння (1). Тоді

f (х) + j (x) = q (x) + j (x), (2)

є одержаним рівнянням.

Нехай х₀ – довільний розв’язок рівняння (1). Підставивши х₀ в рівняння (1), одержимо істинну числову рівність

f (х₀) = j (x₀). (3)

До обох частин істинної числової рівності (3) додамо числовий вираз j (х₀) і одержимо істинну числову рівність на основі властивості 1 § 23 п.2:

f (х₀) + j (х₀) = q (x₀) + j (х₀),

яка означає, що х₀ є розв’язком рівняння (2).

Отже, довільний розв’язок рівняння (1) є розв’язком рівняння (2), тобто рівняння (2) є логічним наслідком рівняння (1).

Нехай тепер х₀ – довільний розв’язок рівняння (2), тоді

f (х₀) + j (x₀) = q (x₀) + j (x₀) (4)

є істинною числовою рівністю. Віднявши від обох частин рівності (4) числовий вираз j (х₀), одержимо істинну числову рівність на основі властивості 1 § 23 п.2:

f (х₀) = q (x₀),

яка означає, що х₀ є розв’язком рівняння (1).

Отже, довільний розв’язок рівняння (2) є розв’язком рівняння (1), тобто рівняння (1) є логічним наслідком рівняння (2).

Таким чином, кожне з рівнянь є логічним наслідком другого, що й доводить їх рівносильність.

Наслідок 1. До обох частин рівняння з однією змінною можна додати (відняти) одне і те ж число, і одержимо рівняння рівносильне даному.

Наслідок 2. Члени рівняння з однією змінною можна переносити з однієї частини рівняння в другу з протилежним знаком, при цьому одержимо рівняння, рівносильне даному.

Наслідок 3. При потребі всі члени рівняння з однією змінною можна перенести в одну з частин рівняння, а друга буде рівна нулю, і одержиться рівняння рівносильне даному.

Теорема 2. Якщо обидві частини рівняння з однією змінною, визначеного на множині М, помножити на вираз, визначений на цій же множині і відмінний від нуля, то одержимо рівняння, рівносильне даному на множині М.

Доведення теореми 2 аналогічне доведенню теореми 1, лише при цьому використовуються властивості 3 і 4 істинних числових рівностей § 23 п.2.

Наслідок 4. Обидві частини рівняння з однією змінною можна помножити (поділити) на одне і те ж число, яке відмінне від нуля, і при цьому одержимо рівняння, рівносильне даному.

Наслідок 5. Рівняння , х Î М, рівносильне рівнянню

f (х) = 0, x Î M.

Задача 3. Не розв’язуючи рівнянь

x – 4 = 3 і х² – 16 = 3(х + 4),

вказати, на яких множинах і на підставі яких тверджень вони рівносильні.

Рівняння

x – 4 = 3 і х² – 16 = 3(х + 4)

визначені на множині дійсних чисел R, тобто їх область визначення М = R. Якщо ліву частину х^2- 16 другого рівняння записати (х – 4)(х + 4), то воно набере вигляду

(х – 4)(х + 4) = 3(х + 4).

Тепер неважко встановити, що друге рівняння одержане з першого рівняння шляхом множення обох його частин на вираз х + 4, який не дорівнює нулю на множині 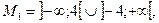а не на множині R. Тому за теоремою 2 про рівносильність рівнянь доходимо висновку, що дані рівняння будуть рівносильними на множині

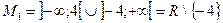
і нерівносильними на множині дійсних чисел R.

При користуванні теоремами 1 і 2 та наслідками з них завжди потрібно пам’ятати, що рівняння рівносильні лише на області визначення вихідного рівняння. Одержане ж рівняння в більшості випадків має ширшу область визначення, отже, може мати і більше розв’язків. Серед них розв’язками вихідного рівняння є тільки ті, що належать його області визначення.

Задача 4. Розв’язати рівняння

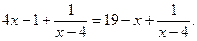
Спочатку встановимо область визначення даного рівняння. Нею буде множина всіх дійсних чисел за винятком числа 4, бо вираз 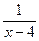при х = 4 не має смислу. Отже, М = R { 4 }. На основі наслідку 3 з теореми 1 перенесемо всі члени даного рівняння в ліву частину, тоді матимемо

Звівши подібні члени, дістанемо рівняння

5x – 20 = 0,

областю визначення якого є вже множина дійсних чисел.

Одержане рівняння має розв’язок х = 4, який не є розв’язком даного рівняння, бо 4 Ï M. Отже, дане рівняння розв’язків не має. Поява стороннього розв’язку для нього пояснюється тим, що внаслідок рівності нулю суми

область визначення одержаного рівняння розширилась, і число 4 ввійшло в неї.

Відповідь: х Ï ø.

Оскільки рівняння з однією змінною є предикатами, то над ними можна виконувати всі операції логіки висловлень, зокрема диз’юнкцію і кон’юнкцію.

Диз’юнкція рівнянь називається сукупністю рівнянь (позначається квадратною дужкою зліва), а кон’юнкція рівнянь – системою рівнянь (позначається фігурною дужкою зліва).

Теорема 3. Рівняння

f₁ (x) × f₂ (x) … f_n (x)=0, х Î М.

рівносильне сукупності рівнянь

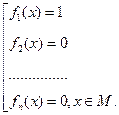
Доведення теореми 3 аналогічне доведенню теорем 1 і 2. Існують різні методи розв’язування рівнянь. Одним із загальних методів розв’язування рівнянь є послідовна заміна їх на рівносильні за допомогою перетворень, що базуються на теоремах 1 і 2 та наслідках з них, поки не прийдуть до рівняння, розв’язки якого легко знайти. Крім того, до таких методів можна віднести зведення рівняння до сукупності рівнянь на основі теореми 3 або спрощення його на основі введення нових змінних. Наприклад, рівняння

(х + 3)(х – 5)(х – 8) = 0

можна розглядати як диз’юнкцію рівнянь

(х + 3) = 0, (х – 5) = 0, (х – 8) = 0,

розв’язки яких легко знайти: – 3, 5, 8. Отже, множина розв’язків вихідного рівняння є об’єднанням множин розв’язків кожного з одержаних рівнянь, а саме { –3, 5, 8}.

Задача 5. Розв’язати рівняння

х⁴ – 4х³ + 8х + 4 – 6(х² – 2х – 2) + 5 = 0.

Дане рівняння можна записати так:

x⁴ – 4х³ + 4х² – 4х² + 8х + 4 – 6(х² – 2х – 2) + 5 = 0 або

(х² – 2х –2)² – 6(х² – 2х – 2) + 5 = 0.

Поклавши х² – 2х – 2 = у, одержимо рівняння

y² – 6у + 5 = 0,

розв’язками якого є у = 1, у = 5. Підставивши ці розв’язки замість у у співвідношення х² – 2х – 2 = у, дістанемо рівняння

х² – 2х – 2= 1 і х² – 2х – 2 = 5,

з яких знаходимо розв’язки даного рівняння:

х₁ = 1, х₂ = 3, х₃ = 1 – 2, х₄ = 1 +2.

Відповідь: х Î {1; 3; 1 – 2, 1+2}.

Дата добавления: 2014-01-13