Лінійні нерівності з однією змінною

Нерівність виду

а₁х + b₁ > a₂x + b₂, a₁, a₂, b_l, b₂, x Î R (1)

називається лінійною нерівністю з однією змінною. Замість знаку ">" можна взяти один із знаків "<", " ³", "£".

Для знаходження розв’язків лінійної нерівності з однією змінною скористаємося наслідками теореми 1 і перенесемо члени, що містять змінну, в ліву частину нерівності, а вільні члени – в праву частину та зведемо подібні члени. Дістанемо нерівність виду

ах > b, (2)

рівносильну нерівності (1).

Якщо а ¹ 0, то лінійна нерівність (2) називається нерівністю першого степеня.

При розв’язуванні нерівності (2) можливі випадки:

1) а > 0, тоді, за наслідком 3 з теореми 2, нерівність (2) буде рівносильною нерівності

а розв’язком якої, а отже, і заданої нерівності, будуть числа проміжку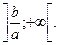

2) а < 0, тоді, за наслідком 4 з теореми 3, нерівність (2) буде рівносильна нерівності

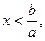
а розв’язками якої, а отже, і заданої нерівності, будуть числа проміжку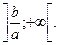

3) а = 0 і b < 0, тоді нерівність (2) матиме вигляд:

0 × х > b,

її задовольняє будь-яке дійсне число, бо добуток нуля і довільного дійсного числа дорівнює нулю, який більший за будь-яке від’ємне число. Отже, в цьому разі нерівність має своєю множиною розв’язків множину дійсних чисел R.

4) а = 0 і b > 0, тоді нерівність (2) матиме вигляд:

0 × х > b

і не матиме розв’язків, бо добуток нуля і довільного дійсного числа дорівнює нулю, який не є більшим за будь-яке невід’ємне дійсне число. Отже, нерівність (2) в цьому разі розв’язків не має.

Задача 2. Розв’язати нерівність

3х + 4 – 6х + 5 > 8x – 3 – 4x + 5.

Користуючись наслідками з теорем про рівносильність нерівностей, будемо мати

3х – 6х – 8х + 4х > –3 + 5 – 4 – 5 Û – 7x > –7 Û х < Û х < 1.

Відповідь: x Î ]–¥; 1[.

Програма початкової школи передбачає лише ознайомлення з поняттям нерівності з однією змінною, розв’язують їх шляхом підбору.

Задача 3. Знайти цілі невід’ємні розв’язки нерівності

2х < 7.

Для знаходження розв’язків даної нерівності скористаємося тим, що її ліву частину можна розглядати як добуток чисел 2 і х. Отже, потрібно знайти цілі невід’ємні числа, добуток яких з числом 2 менший 7. Такими числами є 0, 1, 2 і 3. Таким чином, дана нерівність на множині цілих невід’ємних чисел має чотири розв’язки: 0, 1, 2. 3.

Відповідь: х Î {0,1,2,3}.

Дата добавления: 2014-01-13