Нерівності з двома змінними

Поняття нерівності з однією змінною можна узагальнити на випадок нерівності з кількома змінними. Всі твердження для нерівності з однією змінною матимуть місце і для нерівностей з кількома змінними, тільки відповідно сформульовані. Розглянемо це на прикладі нерівності з двома змінними.

Нехай на множині М_х х М у задано два вирази f (х, у) і q (х, у) з двома змінними х і у. Предикати виду

f (х, у) < q (х, у), f (x,y) > q (x,y),

f (x,y) £ q (x,y), f (x,y) ³ q (x,y), (x,y) Î M_x x M_y,

для яких потрібно знайти області істинності, називаються нерівностями з двома змінними.

Областю визначення нерівності з двома змінними називається область визначення предиката, що її задає. Вона дорівнює декартовому добутку множин М_х і М_у, які є областями визначення змінних х і у відповідно.

Область істинності предиката, що задає нерівність з двома змінними, називається множиною розв’язків нерівності з двома змінними, а впорядкована пара чисел із цієї множини – її розв’язком. Розв’язати нерівність з двома змінними – це означає знайти множину її розв’язків. Знаходження її для нерівностей з двома змінними становить певні труднощі. Тому зручно користуватися геометричним методом, бо за допомогою нього її можна наочно зобразити. Розв’язки нерівності з двома змінними задають певну множину точок на координатній площині, яку визначають за допомогою рівняння, що отримується з даної нерівності заміною її знака на знак рівності. Встановлення цієї множини і становить суть геометричного (графічного) способу розв’язування нерівності з двома змінними. Точки графіка одержаного рівняння будуть належати множині розв’язків даної нерівності тільки тоді, коли вона нестрога. У цьому разі на координатній площині графік рівняння зображається суцільною лінією, в другому – пунктирною.

Розглянемо геометричний спосіб розв’язування нерівності на прикладі нерівності першого степеня з двома змінними виду

ax + by + c > 0, a, b, c Î R,

де а і b одночасно не дорівнюють нулю.

Розв’язавши нерівність відносно однієї зі змінних, наприклад, у, якщо b ¹ 0, дістанемо нерівність

(1)

якщо b > 0, або

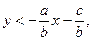(2)

якщо b < 0. Рівняння

визначає на координатній площині пряму, яка ділить площину на дві півплощини: півплощину (І), розміщену вище від прямої, і півплощину (II), розміщену нижче, від прямої (рис. 4).

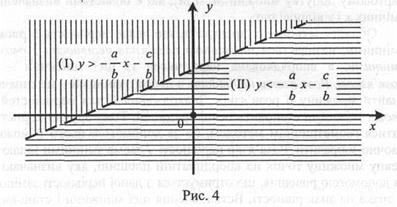
Геометрично множина всіх розв’язків нерівності (1) зобразиться множиною точок півплощини (І), а нерівності (2) – множиною точок півплощини (II).

Кажуть також, що нерівність (1) визначає півплощину (І), а нерівність (2) – півплощину (II).

Дата добавления: 2014-01-13