Симистор

Припустимо на деякому кроці для вибраної підзадачі (zt, Gt) знайдено розв’язок xt. Якщо на попередніх кроках не було знайдено жодного розв’язку підзадачі з М або F(xt) менше усіх значень цільової функції на розв’язках, знайдених на попередніх кроках, значення F(xr) запам’ятовується як поточний рекорд R, а xr - як точка, у якій рекорд досягається.

З утвореної множини М знов вибираємо підзадачу з мінімальною оцінкою, і так далі. Процес утворення підзадач умовно показано деревом на мал. 15.1.

Після кожного розбиття вибраної з множини М задачі утворюються нові задачі, у певному розумінні простіші (з вужчою допустимою областю). Тому на деякому кроці може виявитися, що вибрана підзадача дозволяє очевидним чином отримати її розв’язок або переконатися, що вона розв’язку не має.

Подальше розбиття доцільно виконувати лише для підзадач з оцінкою меншою за R, оскільки очевидно, що коли G_i Ì G_j, то z_i ³ z_j, тобто у результаті розбиття допустимої області оцінка цільової функції не спадає.

На наступних кроках при отриманні для поточної вибраної підзадачі розв’язку x^s, на якому F(x^s) < R, виконується поновлення рекорду:

R = F(x^s), x^r = x^s.

Процес пошуку розв’язку припиняється, якщо множина М не містить підзадачі з оцінкою меншою, ніж R (зокрема, множина М може виявитися і пустою). В результаті, у разі, коли R було обчислено хоча б на одному кроці, x^r – розв’язок задачі, у іншому випадку задача розв’язку не має.

Загальна схема методу гілок та меж

Загальна схема методу гілок та меж має такий вигляд.

1. Обчислити нижню оцінку цільової функції z₀ на допустимій області G і покласти М = {(z₀, G)}, R = , x^r = 0.

2. Якщо М = Æ або М не містить підзадачі з оцінкою меншою R, перейти до кроку 8.

3. Вибрати з М підзадачу з мінімальною оцінкою, вилучити її з М, і якщо вибрана підзадача може бути розв’язана очевидним чином, перейти до кроку 5.

4. Здійснити розбиття вибраної підзадачі на декілька підзадач, ті отримані підзадачі, для яких нижня оцінка менша R, включити у множину М і перейти до кроку 2.

5. Якщо вибрана підзадача розв’язку не має, перейти до кроку 2.

6. Знайти для вибраної підзадачі розв’язок x^t та оптимальне значення цільової функції F(x^t). Якщо F(x^t) ³ R, перейти до кроку 2.

7. Покласти x^r = x^t, R = F(x^t), і перейти до кроку 2.

8. Якщо R< , то x^r - розв’язок задачі, R – мінімальне значення цільової функції, зупинитися.

9. Інакше, задача розв’язку не має, зупинитися.

Наведена загальна схема дає змогу отримати екстремальне значення цільової функції. Але цю схему можна також використати і для пошуку наближеного значення F^* екстремуму цільової функції F_min. Дійсно, у процесі пошуку розв’язку значення рекорду R послідовно зменшується, наближаючись до екстремуму. Тому поточне значення рекорду можна розглядати як наближене значення екстремуму, тобто покласти F^* = R при М ¹ Æ. При цьому виникає питання про ступінь наближення, або про верхню оцінку D відхилення наближенного значення F^* від точного F_min (D ³ F^* - F_min).

Для визначення вказаної оцінки можна скористатися нижніми оцінками цільової функції підзадач, що містяться на поточному кроці у множині М. А саме, якщо позначити мінімальну з нижніх оцінок F(x) для задач з М як z_min, то

F^* - F_min £ F^* - z_min, що і дає шукану оцінку: D = F^* - z_min.

Задача про комівояжера

Розглянемо ще одну відому задачу комбінаторного типу, яка відіграла значну роль у розвитку теорії та методів оптимізації. Саме на цій задачі уперше було продемонстровано застосування методу гілок та меж. Ця задача називається задачею про комівояжера або задачею про китайського листоношу і формулюється таким чином.

Існує n міст, для яких відома матриця транспортних витрат переїзду з кожного міста у кожне C = || c_ij ||_i,j=1 ^m,n, c_ij – вартість переїзду з i-го міста у j-е. Треба скласти маршрут мінімальної вартості, за яким комівояжер, виїжджаючи з деякого міста, проїжджає усі міста і повертається у вихідний пункт. При цьому вважається, що вартість маршруту дорівнює сумі вартостей переїздів, що входять до складу маршруту. Крім того, комівояжер повинен заїзджати у кожне місто тільки один раз, і тому шуканий маршрут являє собою простий цикл.

Побудуємо математичну модель задачі, використовуючи булеві змінні

1, якщо комівояжер з i-го міста переїжджає у j-е;

x_ij =

0 у іншому випадку.

Тоді цільова функція висловлюється таким же виразом, як для задачі про призначення

F = c_ij x_ij ® min. (15.1)

Врахуємо обмеження, згідно з яким комівояжер заїжджає у кожне місто тільки один раз.

x_ij = 1, j = 1, n; (15.2)

Зрозуміло, що і виїжджати з кожного міста комівояжер повинен тільки один раз. Тому уведені змінні задовольняють системі

x_ij = 1, i = 1, n. (15.3)

2 4 5 1 3 6 Мал.15.2. Приклад незв’язного маршруту.

Таким чином отримуємо задачу за формою, співпадаючу із задачею про призначення. Але вказаних обмежень недостаньо для того, щоб змінні відповідали шуканому маршруту. Наприклад, наступна матриця значень x_ij задовольняє обмеженням 15.2, 15.3, але для відповідного маршруту (мал.15.2) порушується властивість зв’язності

0 1 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 1 0 0

Для врахування цього обмеження уведемо змінні x_i, i = 1, n. Будемо надалі вважати, що комівояжер рухається за маршрутом, починаючи з міста 1. Зрозуміло, що останнє припущення не обмежує загальності, оскільки шуканий маршрут є простим циклом.

Тепер доповнимо наведені раніше системи обмежень 15.2, 15.3 такою системою

x_i - x_j + (n – 1)x_ij ≤ n – 2, i,j =2, n, (15.4)

де x_i, x_j - довільні дійсні числа.

У системі 15.4 використовуються змінні, відповідаючі усім містам, крім першого. Покажемо, що жоден незв’язний маршрут не задовольняє цій системі. Припустимо протилежне. Нехай деякий незв’язний маршрут задовольняє системі 15.4. Тоді у цьому маршруті існує цикл, що не проходить через перше місто.

З системи 15.4 виберемо нерівності, відповідаючі переїздам вказаного циклу (x_ij = 1), і знайдемо їх суму. Нехай цикл містить k переїздів. Тоді сума нерівностей має вигляд

(n – 1) k ≤ (n – 2) k, (15.5)

оскільки змінні x_i – взаємно знищуються. Наприклад, для циклу, що проходить через міста 4, 5, 6, маємо

x₄ - x₅ + (n – 1) ≤ n – 2

+ x₅ - x₆ + (n – 1) ≤ n – 2

x₆ - x₄ + (n – 1) ≤ n – 2

(n – 1) 3 ≤ (n – 2) 3.

Оскільки нерівність (15.5) не може виконуватись (є суперечністю), припущення про існування незв’язного циклу, задовольняючого системі 15.4, є хибним.

Тепер покажемо, що зв’язний маршрут задовольняє системі 15.4. Будемо вважати, що змінна x_i дорівнює номеру за порядком відвідування міста i. Наприклад, якщо з міста 1 комівояжер виїжджає у 5-е місто, а потім переїжджає у 4-е, то x₅ = 2, і x₄ = 3. Згідно з припущенням x₁ = 1.

При такому означенні змінних x_i нерівність x_i - x_j ≤ n – 2 виконується для усіх i, j {2, 3, …, n}. Тому при x_ij = 0 нерівності вигляду 15.4 виконуються.

Для x_ij = 1 x_i - x_j = -1, і тому x_i - x_j + (n – 1)x_ij = n – 2. Таким чином, відповідне співвідношення системи 15.4 виконується як рівняння.

Враховуючи отриману математичну модель

F = c_ij x_ij ® min,

x_ij = 1, j = 1, n,

x_ij = 1, i = 1, n.

x_i - x_j + (n – 1)x_ij ≤ n – 2, i,j =2, n,

x_ij = 0 або 1, i,j =1, n,

можна скористатися методом Гоморі, але виявляється, що більш ефективним у поданому випадку є метод гілок та меж.

Розв’язування задачі про комівояжера методом гілок та меж

Будемо вважати допустимою областю задачі множину усіх можливих маршрутів. Кожний маршрут t являє собою набір з n упорядкованих пар:

t = ((i₁, i₂), (i₂, i₃), …, (i_n-1, i_n), (i_n, i₁)),

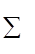у якому кожна пара (i, j) відповідає переїзду з міста i у місто j. Вартіть транспортних витрат F(t) визначається як

F(t) = c_ij. (15.6)

(i, j) t

При застосуванні методу гілок та меж необхідно вирішити два питання:

1) яким чином здійснювати розбиття підзадач;

2) як визначати нижні оцінки цільової функції на допустимих областях підзадач.

Не існує універсального методу пошуку відповіді на ці питання. Все залежить від винахідливості людини, що застосовує метод. Від того, наскільки вдало буде розв’язано ці два питання, залежить ефективність застосування методу.

У конкретному випадку задачі про комівояжера виявилося доцільним розбивати допустиму область підзадачі на дві: одна містить усі маршрути підзадачі з деяким переїздом (i, j) (x_ij = 1), а друга містить усі маршрути без цього переїзду (x_ij = 0).

Для визначення оцінок будемо користуватись приведеними матрицями транспортних витрат, відповідаючими кожній підзадачі. Так саме, як у задачі про призначення, у задачі про комівояжера кожному допустимому розв’язку відповідає сукупність n елементів матриці вартостей c_ij, вибраних таким чином, що у кожному рядку та у кожному стовпчику міститься один елемент. Саме ці елементи підсумовуються у формулі (15.6). Оскільки у приведеній матриці мінімальний елемент кожного рядка і кожного стовпця дорівнює нулю, то очевидною нижньою оцінкою цільової функції для задачі з приведеною матрицею транспортних витрат є нуль.

Значення цільової функції F^’(t) для приведеної матриці відрізняється від значення функції F(t) для вихідної матриці на величину h, що визначається таким чином

h = F(t) - F^’(t) = а_і + bj,

де а_і, bj - суми констант, які віднімалися відповідно від рядків та стовпчиків матриці при приведенні. Враховуючи, що F^’(t) ³ 0, маємо

F(t) = F^’(t) + h ³ h.

Тому величину h можна використати як нижню оцінку цільової функції вихідної задачі. Надалі будемо називати величину h константою приведення.

Тепер після того, як вирішено принципові питання організації процесу розв’язування поданої задачі методом гілок та меж, зробимо ще три важливих зауваження.

Перше зауваження пов’язане з вибором переїзду, за яким виконується розбиття маршрутів на дві підмножини. Будемо вибирати такий переїзд, який, по-перше, має мінімальну вартість, тобто нульову у приведеній матриці, а по-друге, заборона цього переїзду у другій підмножині призводить до максимального збільшення нижньої оцінки цільової функції. Такий принцип розбиття сприяє у більшості випадків найшвидшому отриманню розв’язку задачі.

Друге зауваження пов’язане з врахуванням зв’язності шуканого маршруту. Для того, щоб при виборі поточного переїзду не утворювався незв’язний маршрут (або цикл, що проходить не через усі міста), будемо присвоювати певним елементам матриці витрат значення абстрактного великого числа, що більше будь-якого конкретного, позначаючи його як ¥. Наприклад, якщо для деякої підзадачі вибрані переїзди (i, j), (j, k), (k, l)), то у матриці витрат для поданої підзадачі c_ji = c_kj = c_lk = c_ki = c_lj = c_li = ¥. У вихідній матриці транспортних витрат покладемо c_ii = ¥, i =1, n, заборонивши таким чином переїзд з довільного міста у те ж саме місто.

Нарешті, третє зауваження пов’язане з формою уявлення підзадач та визначенням підзадачі, розв’язок якої очевидний. При виборі переїзду (i, j) (x_ij = 1) у матриці витрат рядок, відповідаючий i-му місту, та стовпець, відповідаючий j-му місту, можна викреслити, оскільки утворена підмножина маршрутів не містить інших переїздів з міста i або у місто j. В результаті, по-перше, утворюється матриця меншого порядку, а по-друге, утворена матриця може виявитися неприведеною, і тоді теба перетворити її у приведену. Це означає, що треба обчислити нове значення константи приведення, або нижньої оцінки цільової функції.

Аналогічно, утворення множини маршрутів без переїзду (i, j) (x_ij = 0, с_ij = ¥) може привести до неприведеної матриці витрат, і тоді матриця перетворюється у приведену, а для константи приведення обчислюється нове значення.

Якщо на поточному кроці вибрана підзадача, якій відповідає матриця витрат розміру 2 х 2, то розв’язок визначається очевидним чином, оскільки така матриця містить тільки два елементи із значеннями, що менше ¥. Ці значення і відповідають переїздам, що треба включити у розв’язок.

Зрозуміло, що кожна підзадача i повністю визначається відповідною матрицею транспортних витрат C_i та відповідною константою приведення h_i.

Алгоритм розв’язування задачі про комівояжера

Алгоритм розв’язування задачі про комівояжера методом гілок та меж має такий вигляд.

1. Для поданої матриці транспортних витрат C побудувати еквівалентну приведену C₀, обчислити відповідну константу приведення h₀ і покласти М = {(h ₀, C₀)}, R = , x^r = 0.

2. Якщо М = Æ або М не містить підзадачі з константою приведення меншою R, перейти до кроку 7.

3. Вибрати з М підзадачу (h_r, C_r) таку, що h_r ≤ h_i, " i | (h_i, C_i) Î М, вилучити її з М: М = М (h_r, C_r), і якщо C_r має порядок 2, перейти до кроку 5.

4. У матриці C_r знайти нульовий елемент c_kl такий, що для будь-якого нульового елементу c_ij виконується умова

min { c_kp } + min { c_ql } ³ min { c_ip } +

" c_km Î C_r & p ¹ l " c_nl Î C_r & q ¹ k " c_im Î C_r & p ¹ j

min { c_qj }.

"c_nj Î C_r & q ¹ i

Побудовати матрицю C_r^*, викресливши у матриці C_r k–й рядок та l–й стовпчик і замінивши значення деяких елементів залишеної частини матриці на ¥ таким чином, щоб заборонити утворення циклів, що проходять через не усі міста. Якщо C_r^* неприведена, побудувати еквівалентну приведену C_r^** і обчислити відповідну константу приведення h^**. Якщо C_r^* приведена, покласти C_r^** = C_r^* і h^** = h_r.

Побудовати матрицю C_r^’, замінивши значення c_kl на ¥, і якщо C_r^’ неприведена, побудувати еквівалентну приведену C_r^’’ і обчислити відповідну константу приведення h^’’ . Якщо C_r^’ приведена, покласти C_r^’’ = C_r^’ і h^’’ = h_r.

Включити у множину М підзадачу (C_r^**, h^**), якщо h^** < R, та підзадачу (C_r^’’, h^’’), якщо h^’’ < R, і перейти до кроку 2.

5. Знайти для вибраної підзадачі розв’язок x^t, доповнивши множину переїздів цієї підзадачі двома переїздами, яким відповідають нульові значення елементів матриці C_r та оптимальне значення цільової функції F(x^t) = h_r. Якщо F(x^t) ³ R, перейти до кроку 2.

6. Покласти x^r = x^t, R = F(x^t), і перейти до кроку 2.

7. x^r - розв’язок задачі, R – мінімальне значення цільової функції, зупинитися.

Оскільки задача про комівояжера завжди має розв’язок, при побудові наведеного алгоритму із загальної схеми методу гілок та меж вилучено кроки, пов’язані з відсутністю розв’язку.

Окремо зупинимося на кроці 4. Величина

w_ij = min { c_im } + min { c_nj }

" c_ip Î C_r & p ¹ j " c_qj Î C_r & q ¹ i

дорівнює збільшенню константи приведення при заміні c_ij = ¥. Тому вказаний вибір нульового елементу у матриці C_r призводить до отримання на поточному кроці другої підзадачі з максимальною нижньою оцінкою цільової функції: h^’’ = h_r + w_kl. Саме ця обставина дозволяє сподіватися на швидше розв’язування задачі, оскільки перехід від кроку 2 до кроку 7 відбувається при виконанні умови R ≤ h_i, " i | (h_i, C_i) Î М.

Приклад розв’язування задачі про комівояжера

Розглянемо приклад розв’язування задачі про комівояжера методом гілок та меж. Нехай комівояжеру необхідно відвідати 4 міста, і вихідна матриця транспортних витрат має такий вигляд.

1 2 3 4 місто в’їзду

1 ¥ 5 3 2 2

2 7 ¥ 1 6 1

3 3 2 ¥ 3 2

4 4 6 2 ¥ 2

місто константи

виїзду

На першому кроці після віднімання від рядків констант, вказаних у стовпчику праворуч, отримуємо

1 2 3 4 місто в’їзду

1 ¥ 3 1 0

2 6 ¥ 0 5

3 1 0 ¥ 1

4 2 4 0 ¥

місто

виїзду

Остання матриця не містить нульового елементу у першому стовпчику, тому для отримання приведеної матриці C₀ треба від елементів цього стовпчика відняти 1. Матриця C₀ має вигляд

1 2 3 4 місто в’їзду

1 ¥ 3 1 0

2 5 ¥ 0 5

3 0 0 ¥ 1

4 1 4 0 ¥

місто

виїзду

Підсумувавши константи, що віднімалися від елементів матриці витрат, отримуємо значення константи приведення h₀ = 2 + 1 + 2 + 2 + 1 = 8, включаємо задачу (h₀, C₀) у множину М: М = {(h₀, C₀ )} і присвоюємо початкові значення R = , x^r = 0.

Від другого кроку переходимо до третього (h₀ < R). На третьому вилучаємо з М задачу (h₀, C₀ ), тепер М = Æ, і переходимо до кроку 4.

На четвертому обчислюємо оцінки w_ij для усіх нулів матриці. Величина w₁₄ дорівнює сумі мінімального елементу першого рядка без c₁₄ та мінімального елементу четвертого стовпця також без c₁₄: w₁₄ = 1 + 1 = 2. Аналогічно, отримуємо w₂₃ = 5 + 0 = 5, w₃₁ = 0 + 1 = 1, w₃₂ = 0 + 3 = 3. w₄₃ = 1 + 0 = 1.

Оскільки максимальну оцінку має елемент c₂₃ , викресливши другий рядок і третій стовпчик, а також зробивши заміну c₃₂ = ¥, отримуємо матрицю C₀^*

1 2 4 місто в’їзду

1 ¥ 3 0

3 0 ¥ 1

4 1 4 ¥

місто

виїзду

Отримана матриця не містить нуля у останньому рядку та у другому стовпчику. Тому для побудови C₀^** віднімаємо від останнього рядка 1, а від другого стовпчика – 3, і отримуємо h₀^** = h₀ + 1 + 3 = 12, та C₀^** у вигляді

1 2 4 місто в’їзду

1 ¥ 0 0

C₀^** = 3 0 ¥ 1

4 0 0 ¥

місто

виїзду

Матриця C₀^’ має вигляд

1 2 3 4 місто в’їзду

1 ¥ 3 1 0

2 5 ¥ ¥ 5

3 0 0 ¥ 1

4 1 4 0 ¥

місто

виїзду

Після приведення отримуємо матрицю C₀^’’

1 2 3 4 місто в’їзду

1 ¥ 3 1 0

2 0 ¥ ¥ 0

3 0 0 ¥ 1

4 1 4 0 ¥

місто

виїзду

і h₀^’’ = h₀ + 5 = 13.

Позначимо C₁ = C₀^**, h₁ = h₀^**, C₂ = C₀^’’, h₂ = h₀^’’, і уведемо задачі (C₁, h₁) і (C₂, h₂) у множину М: М = {(C₁, h₁), (C₂, h₂)}.

Від наступного другого кроку алгоритму переходимо до третього, на якому вилучаємо з М задачу (C₁, h₁), після чого М = {(C₂, h₂)}.

Далі, на четвертому кроці визначаємо: w₁₂ = 0 + 0 = 0, w₁₄ = 0 + 1 = 1, w₃₁ = 1 + 0 = 1, w₄₁ = 0 + 0 = 0, w₄₂ = 0 + 0 = 0, і утворюємо нові дві підзадачі, розбиваючи множину маршрутів відносно переїзду (1, 4).

Для першої підзадачі після викреслення першого рядка та останнього стовпчика і присвоєння c₄₁ = ¥ отримуємо матрицю витрат C₃

1 2 місто в’їзду

3 0 ¥

4 ¥ 0

місто

виїзду

з оцінкою h₃ = 12.

Другій підзадачі відповідає матриця

1 2 4 місто в’їзду

1 ¥ 0 ¥

3 0 ¥ 1

4 0 0 ¥

місто

виїзду

і після приведення її отримуємо матрицю C₄

1 2 4 місто в’їзду

1 ¥ 0 ¥

3 0 ¥ 1

4 0 0 ¥

місто

виїзду

з оцінкою h₄ = 12 + 1 = 13.

Після включення утворених підзадач у М маємо М = {(C₂, h₂), (C₃, h₃), (C₄, h₄)}.

Знов після перевірки умови відбувається перехід від другого кроку до третього, на якому з М вилучається задача (C₃, h₃), оскільки h₃ мінімальна оцінка. Порядок матриці C₃ дорівнює 2, і тому відбувається перехід до кроку 5, на якому отримуємо x^t = ((1, 4), (4, 2), (2, 3), (3, 1)), або x₁₄ = 1, x₄₂ = 1, x₂₃ = 1, x₃₁ = 1 і усі інші x_ij = 0; F(x^t) = 12.

На наступному шостому кроці отримуємо x^r = ((1, 4), (4, 2), (2, 3), (3, 1)), R = 12, і далі від другого кроку (h₂ > R і h₄ > R) відбувається перехід до сьомого кроку, на якому процес розв’язування закінчується.

Симиcmop - полупроводниковый прибор, который широко используется в системах, питающихся переменным напряжением. Упрощенно он может рассматриваться как управляемый выключатель. В закрытом состоянии он ведет себя как разомкнутый выключатель. Напротив, подача управляющего тока на управляющий электрод симистора ведет к переходу его в проводящее состояние. В это время симистор подобен замкнутому выключателю. При отсутствии управляющего тока симистор во время любого полупериода переменного напряжения питания неизбежно переходит из состояния проводимости в закрытое состояние. Кроме работы в релейном режиме в термостате или светочувствительном выключателе, разработаны и широко используются системы регулирования, функционирующие по принципу фазового управления напряжением нагрузки, или, другими словами, плавные регуляторы.

Дата добавления: 2014-01-13