
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекція 17
|
|
|
|
Помножувачі
Множення є одною з найрозповсюдженіших операцій. У багатьох випадках множення здійснюється шляхом послідовного виконання операцій додавання і зсуву впродовж n тактів машинного часу, де n – розрядність операндів. Однак час множення при цьому виявляється надто значним. Тому розроблені різні варіанти швидкодіючих однотактних помножувачів, що випускаються у вигляді окремих мікросхем або входять до складу ВІС як операційні вузли.
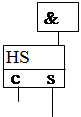
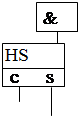
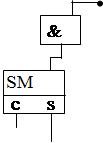
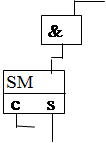
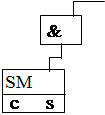
Існують різні типи однотактних помножувачів. Найбільш розповсюджені матричні помножувачі з однорідною структурою (мал.17.1). У такому помножувачі матриця елементів І одночасно формує розряди усіх часткових добутків, що потім підсумовуються за допомогою матриці однорозрядних суматорів. Кожний рядок однорозрядних суматорів перетворює три вхідні доданки у два вихідні. На виході матриці отримують n молодших розрядів добутку p0, p1, …, pn-1 і проміжні значення старших n розрядів (виходи s суматорів n-1-го рядку) та значення одиниць переносу у цих розрядах (виходи с суматорів n-1-го рядку). Таке уявлення старших розрядів у вигляді двох компонент називають двохрядним кодом добутку. Остаточні значення старших n розрядів формуються шляхом підсумовування компонент цього коду за допомогою n-розрядного суматора (на мал.17.1 у штриховому прямокутнику), що вмикається на виході помножувача.
Для підвищення швидкодії матричних помножувачів застосовують алгоритми, дозволяючі одночасно формувати часткові добутки множеного на декілька розрядів множника. Це зменшує кількість часткових добутків і скорочує кількість каскадів однорозрядних суматорів, необхідних для формування двохрядного коду добутку.
   an-1 an-2 a1 a 0 an-1 an-2 a1 a 0
    b0 b0
Мал.17.1. Схема матричного помножувача. |
Одним з найефективніших алгоритмів матричного множення є модифікований алгоритм Бута, зідно з яким формуються часткові добутки множеного А на двохрозрядні групи множника В = bn bn-1 … b1 b0 за формулою Ri = A(-bi+1 2 + bi + bi-1)2i, і = 0, 2, 4, …, n. Застосування цієї формули спрощує обчислення часткових доданків, які можуть приймати значення від - 2А2і до 2А2і. При і = 0, bi-1 = b-1 = 0. Часткові добутки формуються у додатковому коді. Їх підсумовування здійснюється за допомогою матриці однорозрядних суматорів і суматора двохрядного коду добутка, як у помножувачі на мал.17.1.
Для прикладу виконаємо множення чисел А = a3 a2 a1 a0 = 1011 і B = b3 b2 b1 b0 = 1001. Для і = 0 маємо b1 b0 b-1 = 010 і R0 = A = 1011. Для і = 2 b3b2b1 = 100 і R2 = A23 = - 1011000. Додатковий код R2 - 10101000. Для і = 4 b5b4b3 = 001 і R4 = A24 = 10110000. У результаті підсумовування отримуємо 00001011 + 10101000 + 10110000 = 01100011 = А х В.
Реалізація алгоритму Бута дозволяє майже удвічі скоротити кількість каскадів однорозрядних суматорів у схемі додавання часкових добутків, відповідно змешшуючи час множення.
Регістрові блоки
Для проміжного зберігання операндів і результатів операцій широко застосовуються регістрові блоки, що виконують роль зверхоперативних ЗП (кешів). При цьому кожний регістр використовується як комірка пам’яті, зберігаюча багаторозрядне число. Як і у звичайних ОЗП, у таких блоках може бути реалізоване довільне або послідовне вибирання регістрів.
 На мал.10 показана типова структура регістрового блоку (такі блоки часто називають регістровими файлами) з довільним вибиранням, що складається з m n-розрядних регістрів. У режимі запису n-розрядне число D надходить на входи усіх регістрів. Але запис відбувається тільки в один з них, вибір якого здійснюється згідно з надійшовшою адресою (а0 … аk-1), де k log2m. Якщо k = log2m, використовується повний дешифратор, на одному з виходів якого встановлюється сигнал вибирання yі = 1. При цьому сигнал дозволу запису ДЗ = 1 надходить на вибраний регістр, у який заноситься число D. Регістри звичайно реалізуються на D-тригерах. Якщо використовуються D-тригери, що синхронізуються рівнем, сигнал ДЗ подається безпосередньо на вхід синхронізації С. Якщо синхронізація виконується фронтом, синхросигнал подається на окремий вхід синхронізації С (штрихові лінії на мал.10). У режимі читання адреса b0 … bk-1 потрібного регістра надходить на входи багаторозрядного мультиплексора, на виходах якого встановлюється n-розрядне число Q, прочитане з цього регістра. Зв’язки інформаційних входів мультиплексора з усіма регістрами показані на мал.17.2 штриховими лініями. Буферний каскад (БК) з трьома станами при надходженні сигналу дозволу читання ДЧ = 1 передає прочитане число на вихід блоку. Якщо читання заборонене (ДЧ = 0), виходи блоку відключаються від навантаження (реалізується високоомний вихід).
На мал.10 показана типова структура регістрового блоку (такі блоки часто називають регістровими файлами) з довільним вибиранням, що складається з m n-розрядних регістрів. У режимі запису n-розрядне число D надходить на входи усіх регістрів. Але запис відбувається тільки в один з них, вибір якого здійснюється згідно з надійшовшою адресою (а0 … аk-1), де k log2m. Якщо k = log2m, використовується повний дешифратор, на одному з виходів якого встановлюється сигнал вибирання yі = 1. При цьому сигнал дозволу запису ДЗ = 1 надходить на вибраний регістр, у який заноситься число D. Регістри звичайно реалізуються на D-тригерах. Якщо використовуються D-тригери, що синхронізуються рівнем, сигнал ДЗ подається безпосередньо на вхід синхронізації С. Якщо синхронізація виконується фронтом, синхросигнал подається на окремий вхід синхронізації С (штрихові лінії на мал.10). У режимі читання адреса b0 … bk-1 потрібного регістра надходить на входи багаторозрядного мультиплексора, на виходах якого встановлюється n-розрядне число Q, прочитане з цього регістра. Зв’язки інформаційних входів мультиплексора з усіма регістрами показані на мал.17.2 штриховими лініями. Буферний каскад (БК) з трьома станами при надходженні сигналу дозволу читання ДЧ = 1 передає прочитане число на вихід блоку. Якщо читання заборонене (ДЧ = 0), виходи блоку відключаються від навантаження (реалізується високоомний вихід).
   а0 аk-1 а0 аk-1
   
b0 bk-1 ДЧ
RG0 RG1 RGm-1 MUX БК
Мал.17.2. Регістровий блок з довільним вибиранням. |
Регістрові блоки з послідовним вибиранням реалізуються на зсовуючих регістрах статичного або динамічного типу. Приклад такого блоку показаний на мал.17.3. Кількість регістрів дорівнює розрядності чисел n, а кількість розрядів у регістрах – кількості чисел, що можуть одночасно зберігатися у блоці. При ДЗ = 1 число D може заноситися у блок. Занесення відбувається за надходженням фронту синхроімпульсу. Перший синхроімпульс призводить до занесення числа D у перші розряди регістрів. При надходженні наступного синхроімпульсу це число зсовується на один розряд до виходів блоку, а у перші розряди уводиться наступне число. Таким чином уведене число з’явиться на виході через m тактів. При ДЗ = 0 увід наявого числа заборонений, а у перші розряди регістрів переписується число з останніх розрядів. Отже уведені числа можуть зберігатися, циркулюючи у зсовуючих регістрах. Читання певного числа здійснюється, коли воно надходить у останні розряди регістрів. При цьому подається сигнал дозволу читання ДЧ = 1, і число формується на виходах буферного каскаду. При забороні читання (ДЧ = 0) виходи БК переходять у високоомний стан.
БК
    
Мал.17.3. Регістровий блок з послідовним вибиранням. |
Одним з різновидів регістрових ЗП з послідовним вибиранням є стековий ЗП (мал.17.4). У такому ЗП використовуються реверсивні регістри, а напрямок зсуву залежить від значення сигналу завантаження-розвантаження (ЗР). При дозволі роботи стеку (сигнал ДР = 1) зовнішні синхросигнали С надходять на регістри. У режимі завантаження стеку на блок подається сигнал ЗР = 0, при якому регістри приймають у перші розряди зі входу число D = d0 … dn-1, а потім послідовно зсовують його праворуч – на один розряд у кожному такті. Буферний каскад БК при цьому знаходиться у високоомному стані. У режимі розвантаження стеку (ЗР = 1) уведені числа зсовуються ліворуч на один розряд при надходженні кожного сихроімпульсу і послідовно виводяться зі стеку, потрапляючи на виходи БК. У результаті число, прийняте у стек останнім, буде виведено з нього першим. Тому такі ЗП називають стеком типу “останній прийшов – перший пішов” (LIFO: Last In – First Out). На відміну від стеків регістрові ЗП із структурою, показаною на мал.17.3, іноді називають ЗП типу “черга” або “перший прийшов – перший пішов” (FIFO: First In – First Out).
| БК Q0 Q0 d0 С RG0 Qn-1 Qn-1 dn-1 С RGn-1 С ДР ЗР Мал.17.4 Стековий ЗП. |
|
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 779; Нарушение авторских прав?; Мы поможем в написании вашей работы!









 p0
p0




































 p1
p1







 b2
b2














 p2
p2

















 bn-1
bn-1



















 y0 y1 yn-1
y0 y1 yn-1





 С
С





 C C C
C C C








 Q0
Q0










































 d0 … dn-1
d0 … dn-1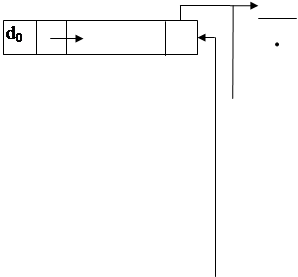








 С
С

















 RGn-1
RGn-1



 ДЗ
ДЗ