Тема 1. Матриці та визначники. Ранг матриці

Розділ 1. Матриці та вектори

План.

1. Поняття матриці. Дії над матрицями та їх властивості.

2. Визначник матриці. Основні властивості визначників.

1. Матрицею розміру m´ n називається таблиця з m×n чисел, яка складається з m рядків та n стовпців. Як правило, вони позначаються великими латинськими літерами.

Наприклад, А=- матриця розміру 2´3.

В загальному випадку матриця має вигляд А=.

Якщо m¹n, то матриця називається прямокутною, якщо m=n, то квадратною з порядком n.

Елементи мариці, в яких i=j складають головну діагональ матриці. Інша діагональ називається побічною.

(a₁₁, a₁₂,....., a_1n)- матриця - рядок, розміром 1´n.

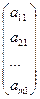- матриця- стовпець, розміром m´1.

Якщо в матриці рядки замінити стовпцями, то отримаємо нову матрицю, яка називається транспонованою до данної.

B=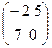; B^T=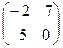- транспонована до B матриця.

Матриця, всі елементи якої дорівнюють нулеві, називається нульовою.

C= - нульова матриця розміром 3´4.

Квадратна матриця називається діагональною, якщо всі її елементи, які не лежать на головній діагоналі дорівнюють нулеві (причому на головній діагоналі можуть бути і нульові елементи).

D= - діагональна матриця розміру 3.

Одиничною матрицею називається діагональна матриця, всі елементи якої рівні 1.

Дві матриці називаються рівними, якщо вони мають однаковий розмір і їх відповідні елементи рівні між собою.

Дії над матрицями.

1. Множення матриці на число.

Добутком матриці А на число a називається матриця, елементи якої є добутком матриці А на число a.

А= ; aA= ;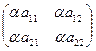

Властивості: 1). aA=Аa;

2). 0А=0;

3). a(bА)=(ab)А.

2. Додавання матриць (додавати можна лише матриці одного розміру).

Сумою двох матриць однакового розміру називається матриця того ж розміру, елементи якої є сумами відповідних елементів матриць.

А=; В=; А+В=+=.

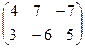Властивості: 1). А+В=В+А.

2). А+0=А.

3). (А+В)+С=А+(В+С).

4). a(А+В)=a А+aВ.

5). (a+b)А=aА+bА.

3. Різниця матриць. А-В=А+(-1)В.

4. Множення матриць. Дві матриці А і В можна множити тільки тоді, коли число стовпців першої матриці дорівнює числу рядків другої матриці.

Нехай маємо дві матриці

А=(m´n), B= (n´p).

Добутком матриці А і В (АВ) називається матриця С, розміром m´p

С=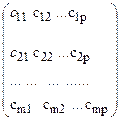, де c_ij=a_i1b_1j+a_i2b_2j+.....+a_inb_nj. i=1,2,...,m; j=1,2,...,p.

Тобто, щоб одержати елемент с_ij, який розміщений в i-ому рядку, в j-ому стовпчику потрібно всі елементи i-ого рядка матриці А перемножити на відповідні елементи j-ого стовпця матриці В і отримані добутки додати.

Властивості: 1) АВ¹ВА (в загальному випадку).

2) АЕ=ЕА=А (де Е- одинична матриця).

3) (АВ)С=А(ВС).

4) А(В+С)=АВ+АС.

5) a(АВ)=(a А)В=А(aВ).

Якщо АВ=ВА, то такі матриці називаються комутативними, наприклад, одинична матриця комутативна з будь - якою свого порядку.

Піднесення до степеня Аⁿ, де nÎN (А в степені n) - можливе лише, коли матриця квадратна і утворюється послідовними добутками. За означенням вважають, що А⁰=Е.

2. Нехай маємо квадратну матрицю другого порядку .

Визначником другого порядку, який відповідає даній матриці, називають число a₁₁a₂₂ - a₁₂a₂₁ і позначають 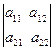= a₁₁ a₂₂ - a₁₂ a_21.

Нехай задана матриця третього порядку .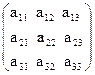

Визначником третього порядку, який відповідає даній матриці називається число

a₁₁ a₂₂ a₃₃ + a₂₁ a₃₂ a₁₃ + a₁₂ a₂₃ a₃₁ - a₁₃ a₂₂ a₃₁ - a₂₁ a₁₂ a₃₃ - a₂₃ a₃₂ a₁₁,

і позначається

.

Властивості визначників:

1) Визначник не зміниться, якщо його рядки замінити стовпцями (стовпці і рядки є рівноправними).

= a₁₁ a₂₂ - a₁₂ a₂₁ і = a₁₁ a₂₂ - a₁₂ a₂₁

2) Якщо поміняти місцями два рядки (стовпці), то визначник змінить знак на протилежний, не змінюючи своєї абсолютної величини.

= a₂₁ a₁₂ - a₂₂ a₁₁ = -(a₁₁ a₂₂ - a₁₂ a₂₁) = - .

3) Якщо у визначнику є два однакових рядки (стовпці), то такий визначник дорівнює нулеві.

Дійсно, нехай визначник D має два однакові рядки. Переставивши їх місцями отримаємо D = - D (за 2-ою властивістю) і, звідси, 2D = 0, D = 0.

4) Якщо всі елементи деякого рядка (стовпця) помножити на одне і теж число, то визначник також помножиться на це число.

= k a₁₁ a₂₂ - k a₁₂ a₂₁ = k(a₁₁ a₂₂ - a₁₂ a₂₁) = k.

Отже, спільний множник всіх елементів деякого рядка (стовпця) можна винести за знак визначника.

5) Визначник, в якому два стовпці пропорційні, рівний нулеві.

Дійсно, коли ми винесемо за знак визначника спільний множник, то отримаємо визначник в якому два однакових рядки (стовпці), а за 3-ою властивістю такий визначник рівний 0.

6) Якщо всі елементи деякого рядка (стовпця) дорівнюють нулеві, то визначник дорівнює нулеві.

Нуль буде множником в кожному з доданків розписаного визначника, отже, і загальний результат 0.

7) Якщо всі елементи деякого рядка (стовпця) є сумою двох доданків, то визначник можна представити у вигляді суми двох визначників.

8) Визначник не зміниться, якщо до всіх елементів деякого рядка (стовпця) додати відповідні елементи іншого рядка (стовпця), помножені на одне і те ж число.

Дата добавления: 2014-01-13