Кодирование (сжатие) аналогового источника сообщений

Аналоговый источник, например речь, является основной услугой в цифровых мобильных системах связи. Речь является случайным нестационарным процессом с меняющейся во времени дисперсией σ² и формой спектральной плотности мощности. Реальные системы построены на упрощенной усредненной стационарной гауссовской модели распределения амплитуд сигнала с нулевым средним и корреляционной функцией (рис.2.2)

(2.12)

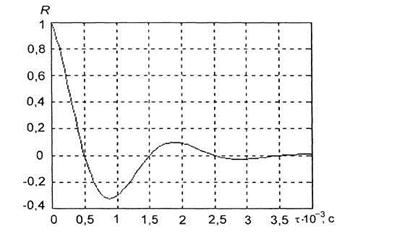
где R(τ) -коэффициент корреляции; τ_к =2·10^-3с; α ≈1,2мс; f₀ =500Гц - частота с максимальной амплитудой в спектре речевого сообщения.

Рис.2.2. Корреляционная функция речевого сообщения.

Спектр речевого сообщения (СПА)

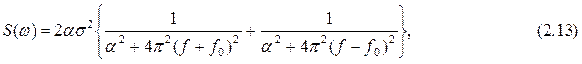
а односторонняя (физическая) спектральная плотность мощности (СПМ) дана на рис.2.3

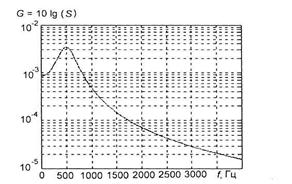Рис.2.3. СПМ речевого сообщения.

Динамический диапазон речевого сигнала в дБ

D=10 lg(σ²_max/ σ²_min ) (2.14)

При цифровой передаче для кодирования со сжатием такого ограниченного по спектру частотой F_B=3кГц сигнала производится его дискретизация по времени и по уровню в преобразователях аналог-код (АЦП).

Дискретизация непрерывных сообщений по времени.

Процесс дискретизации по времени изображен на рис.2.4 и можно представить математической моделью

(2.15)

Если интервалы времени взятия выборок Dt=const, то дискретизация называется равномерной.

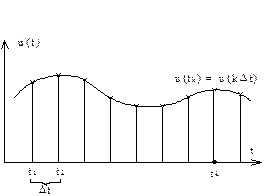
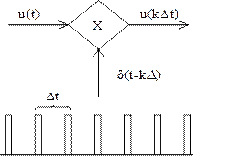
Рис.2.4. Процесс реализации дискретизации по времени.

Для дискретизации сигналов с ограниченным (финитным) спектром известна теореме Котельникова (Найквиста):

“Непрерывная функция времени и(t) со спектром, ограниченным полосой частот от 0 до F_B, полностью определяется последовательностью своих мгновенных значений, взятых в моменты времени, отсчитываемые через интервалы ”,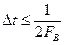

т. е. рядом Котельникова:

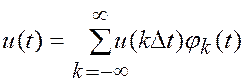, (2.16)

где u(kDt) - значения выборок сообщения в моменты времени kDt, k =0, ±1, ±2...; 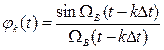- функция отсчётов; Ω_в=2πF_в

Эта функция определена преобразованием Фурье от ортонормированного базиса пространства финитных спектров

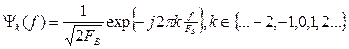,т.е.

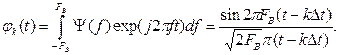
Функция 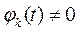только в точке отсчёта t= kDt рис.2.5.

Во всех остальных точках отсчёта t= lDt (l ¹ k) она равна нулю, т.е.

функции отсчётов j_k(t) являются ортогональными

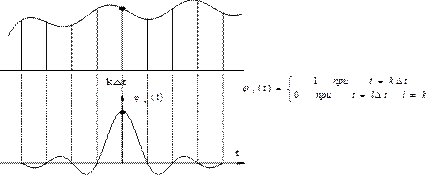Рис.2.5. Функция j_k(t).

Реальные сообщения имеют конечную протяжённость по времени (финитны), поэтому, с этой точки зрения, модель с ограниченным спектром некорректна. Однако, погрешности дискретизации реальных сигналов незначительны. На практике часто берут значение 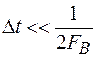, что повышает точность дискретизации с учётом технической реализации.

Для сообщения длительностью T число независимых отсчётов

,

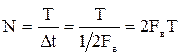называют числом степеней свободы сообщения.

Уместно отметить, что для случайного процесса W(t) с прямоугольным финитным энергетическим спектром (СПМ)

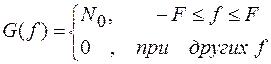
отсчеты U(k∆t) являются случайными величинами с корреляционной функцией (КФ) согласно преобразованию Винера-Хинчина для четной функции:

,

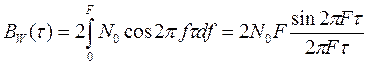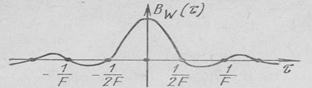Рис.2.6. КФ сигнала с прямоугольной СПМ.

КФ совпадает с функцией отсчетов по Котельникову и равна 0 при τ=±kDt =±k/2F. Таким образом, если спектр сигнала в полосе 0<│f│<F равномерный, то отсчеты случайного сигнала не коррелированны и разложение в ряд Котельникова является каноническим. При неравномерном спектре нельзя утверждать о абсолютной некоррелированности отсчетов, тем более об их независимости для не гауссовских процессов.

Сигнал с финитным спектром u(t) можно точно восстановить по его отсчетам (на выходе ЦАП) в декодере сообщения, если их пропустить через ФНЧ с АЧХ:

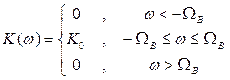(2.16´)

Импульсная характеристика такого ФНЧ имеет вид

.

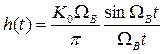Найдем выходной сигнал ФНЧ согласно интегралу Дюамеля, используя модель (2.15):

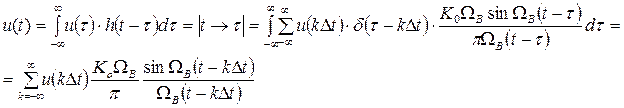т. е. получили на основе фильтрующих свойств δ-функции ряд (2.16) для u(t).

Равномерное скалярное квантование по уровню.

Задачей квантования АЦП является преобразование отсчета

непрерывной СВ U(t) в дискретную по уровню СВ U_д(t_i) с конечным

числом возможных случайных значений { U_дк, k=1,2…M }. При этом используется дискретная характеристика АЦП. Принцип квантования представлен на рис.2.7.

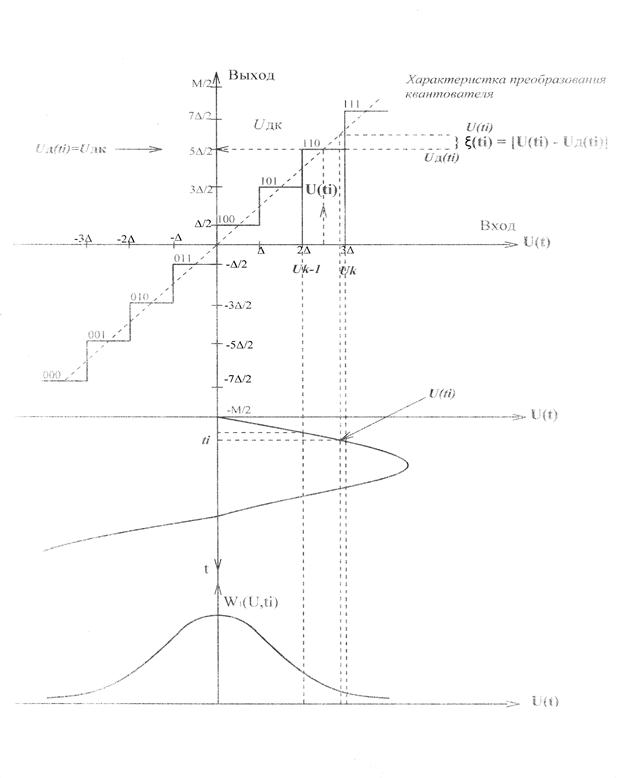
Рис. 2.7. Принцип квантования по уровню и кодирования в АЦП.

Вероятности этих дискретных значений квантователя равны:

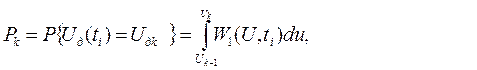
где U_k –уровни квантования по входу квантователя;

U_дk=(U_k+U_k-1)/2 – выходные уровни квантователя;

h _k= Δ = (U_k -U_k-1) –шаг квантования k -го уровня;

W₁(U,t_i)- одномерная плотность вероятности амплитуд отсчета U_i(t_i).

При равномерном квантовании h_k - const для всех k и ошибка квантования

ξ(t_i)=U(t_i)-U_д(t_i)

не зависит от k. Она принимает значения в интервале {-h/2,+h/2} и является непрерывной случайной величиной с распределением, аппроксимируемым равномерным законом на этом интервале. В этом случае среднее значение M[ξ(t_i)]=0, а дисперсия ξ²=h²/12.

В этом случае цифровую последовательность кодового слова АЦП длиной n=log₂М можно представить в виде

U_д(t_i)=U(t_i)+ξ(t_i),

а ошибку квантования рассматривать как аддитивный шум.

Поэтому квантователь (АЦП) характеризуют отношением сигнал/шум квантования (ОСШК, дБ):

ОСШК=10 lg(σ²/ ξ²), (2.17)

где σ² -дисперсия сигнала, например, речевого (2.12) на входе АЦП.

Потенциальные возможности сжатия при скалярном равномерном квантовании речевого сигнала с простой гауссовской моделью (0, σ²) и независимыми отсчетами при заданном значении дисперсии ξ² ошибки квантования определены нижней границей Шеннона для скорости кодирования (числа бит n КС АЦП на отсчет)

(2.18)

Для этой границы найдем зависимость ОСШК от разрядности АЦП. По определению log₂b=a, где b=2^a. Выразим в (2.18) дисперсию ξ² через остальные величины, а результат в дБ.

10 lg(ξ²) =10 lg(2^-2Rs·σ²)= -2 R_s 10 lg 2+10 lgσ² = -6 R_s +10 lgσ² .

Тогда ОСШК (2.17) равно:

ОСШК=10 lg σ² -10 lg ξ² =6 R _s= 6n ., дБ, (2.19)

где n – разрядность АЦП.

Для стандарта ИКМ со скоростью 64 кбит/с, n =8, f_g =8 кГц

ОСШК=6,02 n+ α, где α=4,77 для максимального значения и α=0 для среднего значения этого отношения.

Неравномерное по уровню скалярное квантование.

Если известна плотность вероятности речевого сигнала, то дисперсию ошибки квантования ξ² можно уменьшить неравно-мерным квантованием, т.е. расположением U_д(t_i)=f_кв [ U(t_i) ].

Тогда дисперсию ошибки квантования можно записать в виде

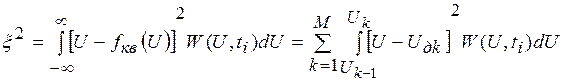
Из этого выражения следует, что для уменьшения дисперсии следует располагать уровни квантования более плотно в участках, где плотность вероятности входного сигнала имеет наибольшее значение и наоборот. Известно, что для речевого сигнала наиболее вероятны малые уровни сигнала. На практике неравномерное квантование реализуют с помощью последовательных операций рис.2.8:

Рис.2.8.Скалярный квантователь с неравномерным шагом квантования.

-равномерное квантование с n =12, f₀ =8 кГц;

-цифровая компрессия до n =8 (компандирование) с помощью

нелинейного безинерционного преобразователя

y=f_комп (x),

где x -значение цифрового сигнала на входе компандера.

Характеристика сжатия компандера по μ -закону имеет вид

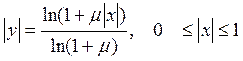
и представлена на рис.2.9.

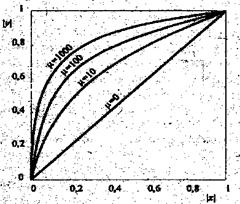Рис.2.9. Характеристика сжатия компандера по μ -закону.

Согласно этому закону при малых значениях речевого сигнала характеристика преобразования близка к линейной и имеет максимальную производную. При больших значениях она является логарифмической или близкой к ней. При восстановлении речевого сигнала в приемнике осуществляется декомпрессия с помощью функции, обратной функции рис.2.9. Такие преобразования эквивалентны неравномерному расположению уровней квантования, т.е. при наиболее вероятных малых уровнях шаг квантования меньше.

Более эффективное сжатие речи реализуется методами ДИКМ и АДИКМ.

Следует отметить:

1. Поскольку скалярный квантователь превращает непрерывную амплитуду отсчета в дискретную, можно трактовать дискретные амплитуды как символы с соответствующими вероятностями { Р_k }. Если они независимы, то на выходе имеем ДИБП с энтропией (2.3)

.

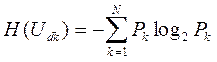2. На основании теоремы об асимптотической равной вероятности укрупненного источника можно ожидать, что блоковое кодирование укрупненного источника приведет к равной вероятности появления слов на выходе такого источника. Это свойство укрупненного источника положено в основу блочного, в частности, векторного квантования речи. Блок из m отсчетов (кодовых слов скалярного квантователя) речевого сигнала на интервале m ∆t образует входной вектор квантователя.

Блочное квантование речевого сигнала.

а) Векторное квантование.

Более высокая эффективность векторного квантования (более низкая битовая скорость) по сравнению со скалярным квантованием достигается за счет модельного кодирования с предсказанием (ЛПК) источника речи и учета статистической зависимости между отсчетами сигнала.

При модельном кодировании источник речи моделируется на основе метода переменных состояния линейным всеполюсным порождающим фильтром с передаточной функцией в Z плоскости

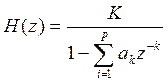
где K -коэффициент усиления фильтра;

- a_k -параметры фильтра (коэффициенты).

Возбуждающими функциями V_n, n =0,1… порождающего фильтра являются последовательности импульсов с периодом Т основного тона для вокализованных блоков или последовательность отсчетов белого гауссовского шума с единичной спектральной плотностью N₀ для не вокализированных блоков (фрагментов речи).

Техническая реализация векторного квантования осуществляется с использованием кодовой книги, в которой хранятся все возможные выходные слова вектора коэффициентов с ортогональными компонентами (независимыми a_k). По входному коррелированному вектору коэффициентов осуществляется поиск в кодовой книге такого выходного вектора коэффициентов, который более близок входному. Векторное квантование может обеспечить меньшую ошибку даже для сигнала с независимыми отсчетами. Выигрыш по сравнению со скалярным возрастает для коррелированных в блоке отсчетов.

б) Адаптивно-преобразующее кодирование (АПК) речи в частотной области.

АПК кодирование речи является разновидностью блочного кодирования. Блок отсчетов речевого источника размером m (с выхода скалярного АЦП) преобразуется на основе, например, БПФ в частотную область. При таком преобразовании отсчеты в частотной области являются близкими к некоррелированным, которые повторно квантуются по уровню и передаются. В декодере приемника декодированная группа спектральных отсчетов преобразуется обратно во временную область и пропускается через ЦАП с ФНЧ и речевой сигнал восстанавливается. При таком кодировании предусматривается больше бит для более важных НЧ спектральных коэффициентов. В кодерах АПК можно получить качественное кодирование при скорости 9000 бит/с.

2.2. Представление колебаний рядами по системе ортогональных функций.

Дата добавления: 2014-01-13