Мощность множества

Два множества называются равномощными, если между их элементами можно установить взаимно-однозначное соответствие.

Два конечных множества равномощны, если они содержат одинаковое число элементов. Количество элементов множества называется его кардинальным числом (мощностью) и обозначается либо card A, либо .

Теорема: Для любых конечных множеств А и В

Доказательство: Пусть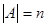

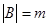
1)

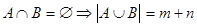
2) Пусть ;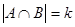

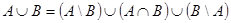
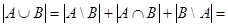
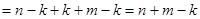
Бесконечное множество называется счетным, если между его элементами и числами натурального ряда можно установить взаимно-однозначное соответствие.

Любые два счетных множества являются равномощными.

Если множество не является счетным, то говорят, что оно несчетное.

Счетное множество является минимальным бесконечным множеством.

Теорема: Если множества A и B счетны, то их декартово произведение тоже счетно.

Доказательство: ;

	a 1	a 2	a 2	¼	an	¼
b 1				…		…
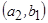
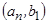
b 2				…		…
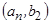
b 2				…		…
…	…	…	…	…	…	…
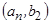
bm				…		…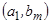
…	…	…	…	…	…	…

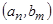
Следствие: Декартово произведение любого конечного числа множеств счетно.

Теорема: Множество точек отрезка счетным не является.

Доказательство:

Любое число, принадлежащее отрезку можно единственным образом представить в виде бесконечной дроби вида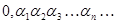

Предположим, что мы сумели перенумеровать все числа отрезка .

Составляем новое число: Это число не принадлежит нашему списку, т.к. отличается от i -го числа в i -м знаке Þ множество точек отрезка счетным не является.

Мощность множества действительных чисел отрезка [0, 1], называемая мощностью континуума, превы­шает мощность счетного множества.

Можно указать множества, мощность которых больше мощности континуума. Но множества с наибольшей мощностью не существует (подобно тому, как не существует наибольшего натурального чис­ла). Это является следствием того, что мощность множества М всег­да строго меньше мощности множества P(М) всех его подмножеств. Иначе говоря, какой бы мощности не было данное множество, всегда можно образовать множество его подмножеств, которое будет иметь большую мощность. Так, Р(N), где N - множество на­туральных чисел, несчетно: его мощность равна мощности конти­нуума.

Дата добавления: 2014-01-13