Спектр тока в цепи с НЭ при кусочно-линейной аппроксимации его характеристики

Пусть суммарное гармоническое и постоянное напряжение вида (4.3) подается на вход электрической цепи с НЭ, характеристика которого аппроксимирована кусочно-линейной линией (рис.4.3) и аналитически описывается формулой:

(4.7)

где 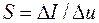- крутизна характеристики.

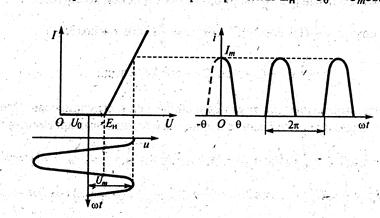
Рис.4.3. Форма тока при кусочно-линейной аппроксимации

характеристики НЭ.

В этом случае временная диаграмма тока, протекающего через НЭ цепи, имеет форму косинусных импульсов с отсечкой их нижней части.

Параметр θ (в радианах или градусах), при котором ток изменяется от максимального значения I_т до нуля, называется углом отсечки. При этом изменение фазы, соответствующее длительности полного импульса тока на выходе цепи, равно 2 θ. Из графиков рис.4.3 нетрудно определить, что при фазовом угле ωt=0, напряжение начала характеристики равно

Е_Н=U₀ + U_mcosθ,

откуда

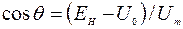. (4.8)

Подставив в формулу (4.7) суммарное напряжение источников сигнала и смещения из выражения (4.3) и напряжение начала характеристики Е_Н, получим аналитическую запись формы тока в зависимости от фазового угла:

(4.9)

Полученную четную функцию i(ωt) периодической последовательности импульсов тока (4.9) можно разложить в тригонометрический ряд Фурье (4.2), в котором период повторения составляет 2π, длительность импульса - 2 θ, а текущей переменной является мгновенный фазовый угол φ=ωt.

Полученные результаты разложения принято записывать в форме:

, (4.10)

где γ_0, γ₁…, γ_п – функции Берга или коэффициенты гармоник, определяющие величины гармоник в спектре преобразованного тока:

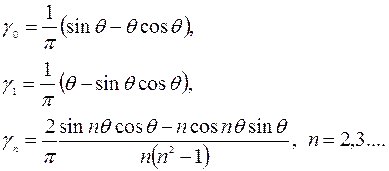(4.11)

Коэффициенты гармоник тока используются в инженерных расчетах, например, нелинейных усилителей мощности, умножителей частоты, преобразователей, автогенераторов и приводятся в специальной литературе в виде таблиц или графиков. На рис.4.4 показаны графики первых трех из этих функций в зависимости от угла θ отсечки тока, которые позволяют выбрать θ для требуемой максимальной гармоники.

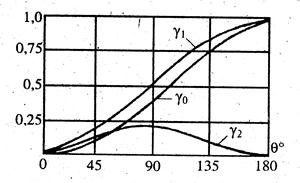
Рис.4.4. Коэффициенты гармоник в зависимости от θ.

Дата добавления: 2014-01-13