Производная по направлению и градиент. Выпуклые функции

Производной 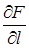функции F (X) = F (x ₁, x ₂, …, x_n) по направлению l в точке Х называется предел

.

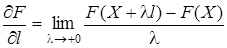Направление l обычно задается вектором l = (l ₁, l ₂, …, l_n).

Если функция F дифференцируема в точке X, то она имеет в этой точке производную по любому направлению l, которая выражается через частные производные по формуле

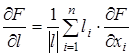, (11.1)

где | l | — длина вектора l, т.е. .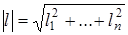

Абсолютная величина производной по направлению дает скорость изменения функции в этом направлении, а знак показывает характер изменения функции (возрастание или убывание).

Градиентом Ñ F функции F (X) = F (x ₁, x ₂, …, x_n) называется вектор, проекциями которого на координатные оси служат соответствующие частные производные, т.е.

.

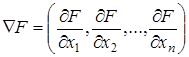Можно показать, что 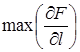достигается тогда, когда направление l совпадает с направлением Ñ F. По формуле (11.1) производная функции F по направлению градиента Ñ F равна

.

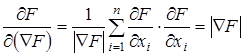Таким образом, в каждой точке Х направление градиента является направлением наибольшего возрастания функции, а длина градиента равна наибольшей скорости возрастания функции в этой точке.

Ñ 11. 1. Найти наибольшую скорость возрастания функции F = x ₁ x ₂ x ₃ + 2 x ₃ в точке A (0; 1; 2) и определить характер изменения этой функции в точке A в направлении l = (1; -2; 2).

Решение. Так как 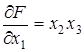, , 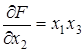, 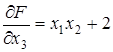то 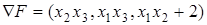и Ñ F | _A = (2; 0; 2). Таким образом, наибольшая скорость возрастания функции в точке A равна 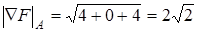. Далее 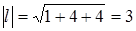и 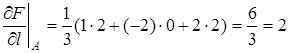. Так как 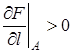, функция F в точке А в направлении l возрастает. Ñ

Напомним (см. разд. 2.2), что множество точек называется выпуклым, если оно вместе с любыми своими двумя точками содержит и весь отрезок, соединяющий эти точки. Если [ a, b ] — отрезок на числовой прямой и x Î [ a, b ], то, как показано в разд. 3.1, x = a а + (1 - a) b, 0 £ a £ 1 или

х = a₁ a + a₂ b, a₁ + a₂ = 1, a₁³ 0, a₂ ³ 0. (11. 2)

Нетрудно видеть и обратное: если выполняется (11.2), то x Î [ a, b ]. Таким образом, отрезок [ a, b ] можно определить как множество всех точек x, удовлетворяющих условию (11.2). Тогда выпуклое множество — это множество, которое вместе с любой парой своих точек a, b содержит и все точки x, для которых выполняется (11.2). Эти определения отрезка и выпуклого множества сохраняются для случая, когда а, b, x — точки n -мерного пространства (где операции в равенстве (11.2) выполняются покоординатно).

Исходя из равенства (11.2), по индукции можно показать, что если М — выпуклое пространство, то для любых точек X ₁, …, X_r Î M и любых действительных чисел t_i ³ 0, удовлетворяющих условию .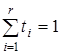

Функция F (X) = F (x ₁, …, x_n), определенная на выпуклом множестве М n-мерного пространства, называется выпуклой на этом множестве, если

F (a X ₁ + (1 - a) X ₂)£a F (X ₁) + (1 - a) F (X ₂) (11. 3)

для любых точек Х ₁, Х ₂Î М и любого числа a Î [0; 1].

Если в условии (11.2) изменить знак неравенства £ на ³, то получим определение вогнутой функции. Если же в условии (11.3) неравенство выполняется как строгое, то функция называется строго выпуклой (или строго вогнутой).

На рис. 11.1 изображен график функции одной переменной, выпуклой на всей числовой прямой.

Для любой пары X ₁, X ₂ значений аргумента произвольную точку Х Î [ X ₁, X ₂](см. (11.2)) можно задать в виде Х = a X ₁ + (1 - a) Х ₂. Как видно из рис. 11.1, неравенство (11.3) означает, что отрезок, соединяющий точки (X ₁; F (X ₁)) и (X ₂; F (X ₂)) расположен не ниже графика функции на этом участке (для строго выпуклой функции этот отрезок лежит выше графика). Таким образом, выпуклость или вогнутость функции одной переменной сразу же видна по ее графику.

Ñ 11. 2. Установить выпуклость (вогнутость) функций, приведенных на рис. 11.2.

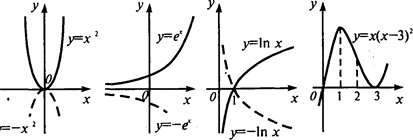
Рис. 11. 2

Решение. Функции у = х ² и у = e^х являются всюду строго выпуклыми, а у = lп х строго вогнута на интервале (0; ¥). Функция у = x (x - 3)² не является ни выпуклой, ни вогнутой на всей числовой прямой, но точка x = 1 разбивает ее на два участка: слева от этой точки она вогнута, справа — выпукла (рис. 11.2). Ñ

Рассмотрим свойства выпуклых функций. Все рассматриваемые функции предполагаются определенными на некотором выпуклом множестве М. Свойства приводятся без доказательств, но многие из них легко проверяются по определению (11.3) и для функций одной переменной иллюстрируются графиками.

Алгебраические и аналитические свойства выпуклых функций:

1. Если функция F (X) выпукла, то функция -F (X) вогнута.

2. Функция F (X) = С и линейная функция F (X) = aХ + b являются всюду выпуклыми и всюду вогнутыми.

3. Если функции F_i (X), i = 1, …, m, выпуклы, то при любых действительных числах a _i ³ 0 функция 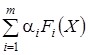также является выпуклой.

4. Если функция F (Х) выпукла, то для любого числа a область решений неравенства F (X) < a является либо выпуклым множеством, либо пустым.

Отметим следствия свойства 4 и теоремы о пересечении выпуклых множеств.

5. Если функции j _i (X) выпуклые при всех неотрицательных значениях переменных, то область решений системы неравенств j _i (Х) £ b, i = 1, …, m является выпуклым множеством (если она не пуста).

6. Выпуклая (вогнутая) функция, определенная на выпуклом множестве М, непрерывна в каждой внутренней точке этого множества.

7. Всякая дифференцируемая строго выпуклая (вогнутая) функция имеет не более одной стационарной точки (т.е. точки, е которой равны нулю все частные производные). При этом для выпуклой (вогнутой) функции стационарная точка всегда является точкой локального и глобального минимума (максимума).

8. Дважды дифференцируемая функция F (X) = F (x ₁, …, x_n) является выпуклой в том и только в том случае, когда

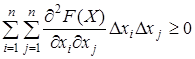(11.4)

для любых Х Î М и D x_i, D x_j, не обращающихся в нуль одно временно.

Чтобы использовать это условие для определения выпуклости конкретной функции, часто бывает полезен критерий Сильвестра: условие (11.4) выполняется тогда и только тогда, когда неотрицательны все главные миноры D _k матрицы вторых частных производных, т.е. определители

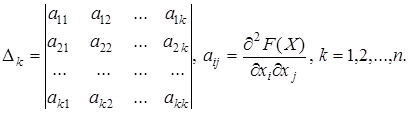(11.5)

Если все D _k > 0, то неравенство (11.4) выполняется как строгое, и тогда функция F является строго выпуклой.

Ñ 11. 3. Показать, что следующие функции являются выпуклыми:

а) ;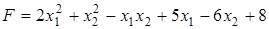

б) .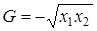

Решение. а) Находим частные производные: 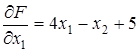, , 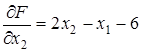, , 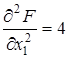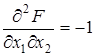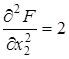. Матрица вторых частных производных имеет вид 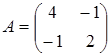. Ее главные миноры D₁ = | 4 | = 4 > 0, D₂ = | А | = 7 > 0. Значит, на основании свойства 8, функция F является строго выпуклой при всех X.

б) Здесь 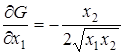, , 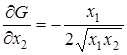, , 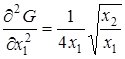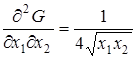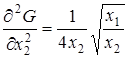. Матрица вторых частных производных имеет вид:

; , .

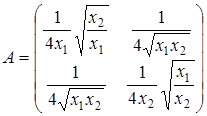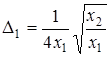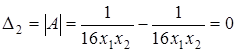Таким образом, G является выпуклой, но не строго выпуклой функцией при x ₁ > 0, x ₂ > 0. Ñ

Дата добавления: 2014-01-13