
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Элементы Фурье-оптики. Групповая скорость
|
|
|
|
В большинстве случаев свет распространяется не в виде плоской монохромной волны 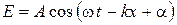 ,
,
где 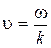 - фазовая скорость,
- фазовая скорость,  - волновой вектор
- волновой вектор
а в виде суперпозиции волн, которые практически не отличаются частотой. Такая суперпозиция волн называется волновым пакетом или группой волн.
Согласно теореме Фурье световой импульс, используемый для передачи сигнала, можно представить как наложение волн, частоты которых заключены в некотором интервале Δω. В фиксированный момент времени пакет имеет длину  . В пределах длины пакета волны в различной степени усиливают друг друга, а вовне – гасят. Расчеты показывают, что чем меньше ширина пакета, тем больший интервал частот Δω требуется для его описания. Имеет место соотношение
. В пределах длины пакета волны в различной степени усиливают друг друга, а вовне – гасят. Расчеты показывают, что чем меньше ширина пакета, тем больший интервал частот Δω требуется для его описания. Имеет место соотношение  .
.
В диспергирующей среде, в отличие от недиспергирующей, пакет с течением времени расплывается, ширина его увеличивается из-за разных фазовых скоростей, составляющих его волн. Если дисперсия невелика, то пакет расплывается медленно и пакету можно приписать скорость, с которой перемещается центр пакета, точка с максимальным значением E. Эту скорость называют групповой скоростью.
 (4.1)
(4.1)
Из этого, так как  , получим:
, получим:  ;
;
Так как k – функция  , то
, то  . Учитывая, что
. Учитывая, что  ,
,

 , поэтому
, поэтому  . Следовательно, групповая скорость может быть записана:
. Следовательно, групповая скорость может быть записана:

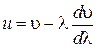 (4.2)
(4.2)
В зависимости от значения  групповая скоростьможет быть больше или меньше фазовой. Понятие групповой скорости применимо только при условии, что поглощение энергии в данной среде невозможно. В области аномальной дисперсии поглощение очень велико и понятие групповой скорости неприменимо.
групповая скоростьможет быть больше или меньше фазовой. Понятие групповой скорости применимо только при условии, что поглощение энергии в данной среде невозможно. В области аномальной дисперсии поглощение очень велико и понятие групповой скорости неприменимо.
Элементарная теория дисперсии
Из макроскопической электромагнитной теории Максвелла следует, что  Для большинства прозрачных сред m = 1, поэтому
Для большинства прозрачных сред m = 1, поэтому  . Отсюда выявляются некоторые противоречия: величина n, являясь переменной, остается в то же время равной определенной постоянной. Кроме того значения n, получаемые из этого выражения, не согласуются с опытом. Трудности объяснения дисперсии света с точки зрения электромагнитной теории Максвелла устраняются электронной теорией Лоренца. В теории Лоренца дисперсия света рассматривается как результат взаимодействия электромагнитных волн с заряженными частицами, входящими в состав вещества и совершающими вынужденные колебания в переменном поле волны.
. Отсюда выявляются некоторые противоречия: величина n, являясь переменной, остается в то же время равной определенной постоянной. Кроме того значения n, получаемые из этого выражения, не согласуются с опытом. Трудности объяснения дисперсии света с точки зрения электромагнитной теории Максвелла устраняются электронной теорией Лоренца. В теории Лоренца дисперсия света рассматривается как результат взаимодействия электромагнитных волн с заряженными частицами, входящими в состав вещества и совершающими вынужденные колебания в переменном поле волны.
Под действием поля Е световой волны электронные оболочки атомов деформируются, т.е. они становятся диполями с моментами 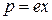 , где е – заряд электрона, х – смещение электрона под действием электрического поля световой волны. Если в единице объема N атомов, то дипольный момент:
, где е – заряд электрона, х – смещение электрона под действием электрического поля световой волны. Если в единице объема N атомов, то дипольный момент:
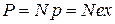
Зная Р, можно вычислить e среды:
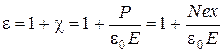 (4.3)
(4.3)
Найдем смещение электрона x под действием внешнего поля волны. В первом приближении можно считать, что вынужденные колебания совершают только оптические электроны, наиболее слабо связанные с ядром атома.
Уравнение вынужденных колебаний электрона запишем на основании 2-го закона Ньютона: 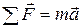 . Учтем, что на электрон будут действовать силы:
. Учтем, что на электрон будут действовать силы:
1. Квазиупругая сила, возвращающая (удерживающая) электрон в состоянии покоя  .
.
2. Сила трения излучения 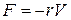
3. Внешняя периодическая сила  , где
, где 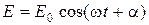
 ,
,  ,
, 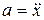 или
или
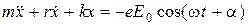 (4.4)
(4.4)
Пренебрежем для простоты расчетов силой трения излучения:
 ,
,
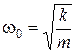 - собственная частота колебаний электрона
- собственная частота колебаний электрона
Из механики известно, что решением этого дифференциального уравнения является выражение:  (4.5)
(4.5)
где  - амплитуда вынужденных колебаний электрона.
- амплитуда вынужденных колебаний электрона.
Подставляя (4.5) в (4.3), окончательно получим:
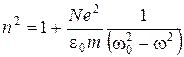 (4.6)
(4.6)
Из (4.6) следует, что при приближении частоты электромагнитной волны ω к собственной частоте электронов в молекуле справа и слева показатель преломления стремиться к  или
или  , соответственно. Это происходит потому, что мы пренебрегли трением излучения. Учет этой силы приводит к зависимости
, соответственно. Это происходит потому, что мы пренебрегли трением излучения. Учет этой силы приводит к зависимости  от w, показанной на рисунке.
от w, показанной на рисунке.
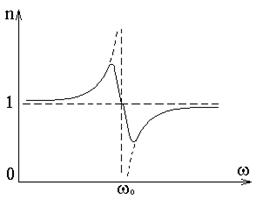
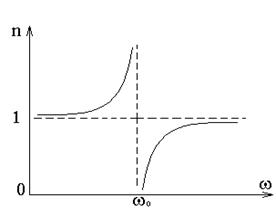 Таким образом, вблизи собственной частоты функция
Таким образом, вблизи собственной частоты функция  терпит разрыв, в этой области наблюдается сильное поглощение электромагнитных волн.
терпит разрыв, в этой области наблюдается сильное поглощение электромагнитных волн.
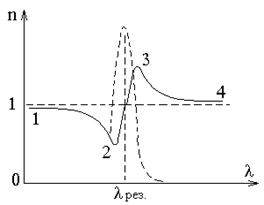 Если перейти от зависимости
Если перейти от зависимости  к зависимости
к зависимости  , то получим кривую несколько иного вида (рис.). Пунктирная кривая характеризует поглощение света в области данной длины волны
, то получим кривую несколько иного вида (рис.). Пунктирная кривая характеризует поглощение света в области данной длины волны  раз. Участки 1-2 и 3-4 – нормальная дисперсия: n убывает с ростом λ и
раз. Участки 1-2 и 3-4 – нормальная дисперсия: n убывает с ростом λ и 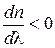 . На участке 2-3 наблюдается аномальная дисперсия
. На участке 2-3 наблюдается аномальная дисперсия  n растет с ростом λ. Кроме того, легко заметить, что на участке 1-2
n растет с ростом λ. Кроме того, легко заметить, что на участке 1-2 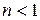 , следовательно, фазовая скорость волны будет больше скорости света в данной среде.
, следовательно, фазовая скорость волны будет больше скорости света в данной среде.
 Если вещество состоит из нескольких сортов атомов, то дисперсионная кривая распадается на ряд ветвей, т.е. каждому сорту атомов своя частота поглощения.
Если вещество состоит из нескольких сортов атомов, то дисперсионная кривая распадается на ряд ветвей, т.е. каждому сорту атомов своя частота поглощения.
Эффект Доплера (см).
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 1374; Нарушение авторских прав?; Мы поможем в написании вашей работы!