Лекція 4.2. Власні значення та власні вектори

Контрольні запитання

1. Який векторний простір називається лінійним?

2. Перерахуйте властивості операцій, визначених на лінійних просторах.

3. Що є матрицею переходу між двома базисами лінійного простору?

4. Що називається лінійним перетворенням?

5. Дайте означення тотожного лінійного перетворення.

6. Які дії можна виконувати над лінійними перетвореннями?

7. Які лінійні перетворення називаються оборотними, оберненими?

8. Що таке невироджене лінійне перетворення?

План

1. Власні значення та власні вектори.
2. Евклідів простір та його властивості.
3. Ортогональний базис та ортогональне перетворення.

1. Кажуть, що матриця А=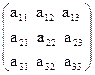задає лінійне перетворення, якщо для двох векторів та 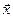справджується рівність

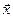=А (1)

Довільний ненульовий вектор 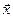називається власним вектором лінійного перетворення, заданого матрицею А, якщо знайдеться таке число l, що виконується рівність А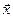=l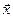. Число l при цьому називається власним значенням лінійного перетворення А. З означення видно, що при перетворенні вектор 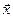переходить у колінеарний йому вектор l.

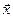Нехай власний вектор 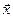=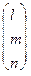. Тоді рівність (1) набуде вигляду: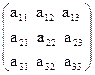 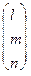=l,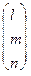

або, на основі рівності двох матриць,

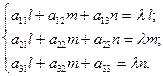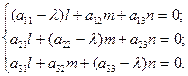Ю (2)

З цієї системи необхідно визначити координати l, m, n. Так як 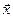- ненульовий вектор, то хоч одна з цих координат нерівна нулю, тобто, система має нетривіальний розв’язок. Однорідна система має ненульовий розв’язок тоді і тільки тоді, коли її визначник рівний нулю, то

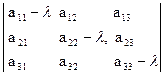=0. (3)

Рівняння (3) називається характеристичним рівнянням матриці А лінійного перетворення (1). Розв’язуючи рівняння (3) знаходимо l, а після того розв’язуючи систему (2) знаходимо координати власного вектора 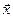. Якщо значень l є кілька, то і власних векторів є кілька.

Приклад 1. Знайти власні вектори і власні значення, лінійного перетворення, заданого матрицею

А=.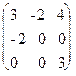

Розв’язування.

Складемо характеристичне рівняння: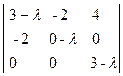=0.

Розкладемо за елементами третього рядка

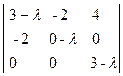=(3-l)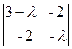=(3-l) ((l-3)l-4)=0.

Власними значеннями матриці є l₁ = -1; l₂ = 3; l₃=4.

Підставимо власне значення l₁ = -1 в систему (2) і отримаємо:

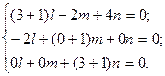
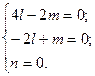
Отже, власним вектором, що задовольняє власне значення l₁ = -1, є довільний вектор вигляду 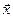=(l, 2l, 0).

Аналогічно знаходимо два інші власні вектори.

2. Лінійний простір R називається евклідовим, якщо є правило, що дозволяє для кожних двох векторів 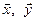з цього простору дійсне число, що називається скалярним добутком векторів і позначається 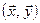, причому це правило задовольняє умови:

1) ;

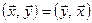2) ;

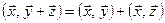3) для довільного дійсного числа .

4) 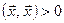, якщо .

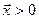З вищеперерахованих умов випливають наслідки:

а) ;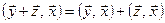

б) ;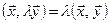

в) 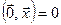для довільного вектора .

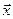Скалярний добуток будь якого вектора самого на себе називається скалярним квадратом цього вектора.

Довжиною вектора 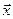в евклідовому просторі називається квадратний корінь із скалярного квадрата цього вектора, тобто .

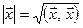Якщо – довільне дійсне число, а 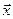– довільний вектор цього простору, то .

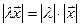Вектор довжина якого рівна 1 називається нормованим.

Для довільних векторів 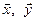із евклідового простору виконується нерівність Коші-Буняковського: 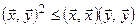. Рівність 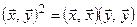має місце тоді і тільки тоді, коли вектори є лінійно залежними.

З нерівності Коші-Буняковського випливає, що 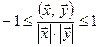. Кут 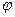, що визначається рівністю 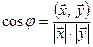і належить відрізку 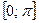, називається кутом між векторами 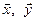. Якщо 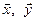– ненульові вектори, а 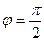, то 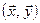=0. В цьому випадку кажуть, що вектори 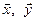є ортогональними і пишуть .

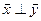Для двох довільних векторів евклідового простору справджуються також нерівність трикутника та теорема косинусів і теорема Піфагора, як наслідок з неї.

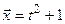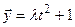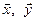Приклад 2. У евклідовому просторі неперервних функцій із визначеним скалярним добутком розглядаємо два вектори , . Знайти таке значення , при якому вектори ортогональні на відрізку 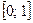і перевірити справедливість теореми Піфагора для цих векторів.

Розв’язування. Складемо скалярний добуток:

.

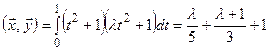З умови 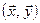=0 визначаємо .

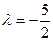Знайдемо тепер довжини векторів 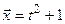, 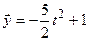та :

,

,

.

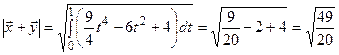Таким чином, теорема Піфагора справджується.

3. Базис векторів евклідового простору називається ортогональним, якщо при довільних справджується рівність .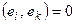

Справедлива теорема: у всякому евклідовому просторі є ортогональний базис.

Якщо ортогональний базис складається із нормованих векторів, то він називається ортонормованим. Для ортонормованого базису справджуються рівності:

Довільний вектор 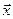евклідового простору, заданий в ортонормованому базисі, визначається рівністю

.

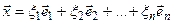Довжина вектора визначається як корінь квадратний із суми квадратів його координат.

Два вектори називаються лінійно незалежними (колінеарними, пропорційними) тоді і тільки тоді, коли їх координати пропорційні.

Умовою ортогональності двох векторів є рівність їх скалярного добутку нулеві.

Кут між векторами шукається аналогічно як кут між векторами у дво та тривимірному просторі.

Нехай дано систему векторів , ,…, 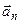в деякому базисі 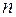-вимірного евклідового простору:

= + +…+ , = + +…+ ,…,

= + +…+ .

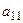
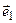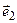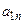
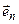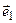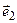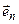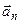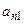
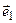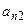
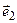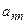
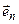Побудуємо визначник із скалярних добутків векторів:

.

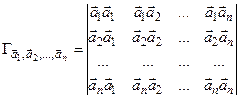Цей визначник називається визначником Грама (Йорген Грам (1850-1916) – датський математик).

Внаслідок того, що для скалярного добутку справедливим є переставний закон (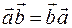), то визначник Грама буде симетричний відносно головної діагоналі.

Справедливою є теорема, яка тут подається без доведення. Для того, щоб система векторів , ,…, 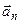була лінійно незалежною, необхідно і достатньо, щоб визначник Грама був додатним

Приклад 3.Довести лінійну незалежність векторів:

= (1; 1; 1), = (1; 2; 1), = (3; 2; 1).

Розв’язування. Визначник Грама: .

Знаходимо кожний із скалярних добутків:

; ;

; ;

; .

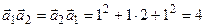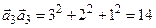Таким чином, визначник Грама має вигляд:

.

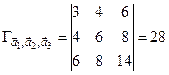Оскільки 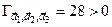, то робимо висновок: вектори лінійно незалежні.

Дата добавления: 2014-01-13