
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекція 4.3. Квадратичні форми та зведення їх до канонічного вигляду
|
|
|
|
План
- Перетворення системи координат.
- Алгебраїчні лінії другого порядку.
- Зведення квадратичних форм до канонічного вигляду.
1. Вибором прямокутної декартової системи координат на площині встановлюється взаємно-однозначна відповідність між впорядкованими парами чисел і точками площини. Вибір системи координат в значній мірі довільний і в різних системах одна і та ж точка площини має різні координати, а одна і та ж лінія (множина точок) визначається різними рівняннями, оскільки рівняння визначає не лише лінію, як геометричний образ, але і її розміщення на площині відносно вибраної нами системи координат. Багато висновків, доведень, розв’язків задач аналітичної геометрії значно спрощуються шляхом перетворення системи координат.
Перехід від однієї системи координат до якої-небудь іншої називається перетворенням системи координат.
Розглянемо два випадки перетворення однієї прямокутної системи координат в іншу.
Паралельне перенесення осей координат. Порівняємо координати однієї і тієї ж точки M, віднесеної до двох систем координат: старої Oxy і нової  . Виберемо системи координат таким чином, щоб осі нової системи були паралельні осям старої системи координат і однаково з ними направлені. Положення нової системи координат відносно старої визначаються координатами нового початку O відносно старої системи.
. Виберемо системи координат таким чином, щоб осі нової системи були паралельні осям старої системи координат і однаково з ними направлені. Положення нової системи координат відносно старої визначаються координатами нового початку O відносно старої системи.
Нехай a і b – координати нового початку 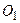 відносно старої системи і нехай яка-небудь точка M має в старій системі координати x і y, а в новій
відносно старої системи і нехай яка-небудь точка M має в старій системі координати x і y, а в новій  і
і  .
.
|O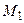 | = x = a +
| = x = a +  і |
і |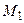 M| = y = b +
M| = y = b +  .
.
Таким чином, формули переходу від старої системи координат до нової і, навпаки, мають вигляд:

| 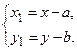
|
Приклад 1. Спростити рівняння другого порядку  до простішого вигляду шляхом паралельного перенесення початку координат.
до простішого вигляду шляхом паралельного перенесення початку координат.
Розв’язування. Визначимо рівняння, якщо початок координат перенести в деяку точку 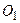 (a, b) площини, а нові осі координат будуть паралельні до відповідних старих. Формули перетворення в цьому випадку матимуть вигляд:
(a, b) площини, а нові осі координат будуть паралельні до відповідних старих. Формули перетворення в цьому випадку матимуть вигляд:

де  і
і 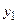 – нові координати.
– нові координати.
Підставляючи значення виразів x і y в рівняння другого порядку, отримаємо рівняння в нових координатах:
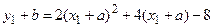 , або
, або 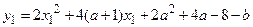 .
.
Для визначення a і b прирівняємо до нуля коефіцієнт при  в першому степені і вільний член рівняння, тобто, розв’язуємо систему рівнянь:
в першому степені і вільний член рівняння, тобто, розв’язуємо систему рівнянь:

Таким чином, ми отримали систему двох рівнянь з двома невідомими a і b. Розв’язуючи цю систему, отримаємо a = –1, b = –10.
При таких значеннях координат a і b початку нової системи координат відносно старої системи рівняння другого порядку описує параболу  , графік якої зміщений відносно осей координат.
, графік якої зміщений відносно осей координат.
Таким чином, відносно нових осей координат рівняння параболи набуває простого вигляду: віссю параболи є вісь 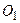
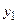 , а вершина знаходиться в точці
, а вершина знаходиться в точці 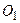 (0, 0). В старій же системі Oxy віссю параболи є пряма з рівнянням x = –1, а вершина параболи знаходиться в точці
(0, 0). В старій же системі Oxy віссю параболи є пряма з рівнянням x = –1, а вершина параболи знаходиться в точці 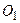 (–1, –10).
(–1, –10).
Поворот осей координат. Нехай тепер нова система координат  утворюється із старої системи Oxy
утворюється із старої системи Oxy 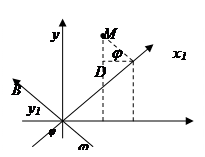 шляхом повороту її навколо початку координат O на кут j. Кут повороту j будемо вважати додатним, якщо поворот від осі Ox до осі O
шляхом повороту її навколо початку координат O на кут j. Кут повороту j будемо вважати додатним, якщо поворот від осі Ox до осі O здійснюється проти напрямку руху стрілки годинника, і від’ємним – в протилежному напрямку. Координати довільної точки M відносно старої системи координат будуть x і y, а відносно нової
здійснюється проти напрямку руху стрілки годинника, і від’ємним – в протилежному напрямку. Координати довільної точки M відносно старої системи координат будуть x і y, а відносно нової  і
і  . На мал. OA = x, AM = = y, OB =
. На мал. OA = x, AM = = y, OB =  , BM =
, BM =  .
.
Враховуючи те, що
OA=OC–AC=OC–DB,
AM=AD+DM=CB+DM,
з трикутників OBC і BDM маємо:
OC = OBcosj = cosj, CB=OBsinj=
cosj, CB=OBsinj= sinj,
sinj,
DM=BMcosj= cosj, DB=BM sinj =
cosj, DB=BM sinj =  sinj.
sinj.
Підстановка значень OC, CB, DM, DB в рівняння системи визначає формули переходу від старих координат до нових при повороті осей на кут j (без зміни початку координат) і, навпаки:
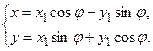
| 
|
Приклад 2. Шляхом повороту осей координат перейти до іншого вигляду рівняння гіперболи xy = 2.
Розв’язування. Формули переходу
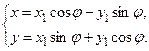
до нової системи координат з новими координатами  і
і  підставляємо у рівняння гіперболи: (
підставляємо у рівняння гіперболи: ( cos j –
cos j –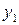 sinj) (
sinj) ( sin j +
sin j +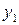 cosj) = 2.
cosj) = 2.
Звівши подібні члени, перепишемо рівняння у вигляді
(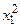 –
–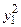 )sin2j +2
)sin2j +2
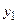 cos2j = 4.
cos2j = 4.
Вибираємо кут j так, щоб коефіцієнт при добутку невідомих 
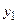 дорівнював нулю: 2cos2j = 0
дорівнював нулю: 2cos2j = 0 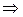 cos2j = 0
cos2j = 0 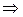 j =
j =  . При такому значенні кута рівняння гіперболи матиме вигляд:
. При такому значенні кута рівняння гіперболи матиме вигляд: 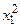 –
–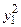 = 4, або
= 4, або 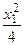 –
– = 1.
= 1.
Рівняння описує гіперболу в системі координат, осі якої повернені, відносно старої системи координат, на 45 проти стрілки годинника.
проти стрілки годинника.
2. Алгебраїчні лінії другого степеня. Розглянуті раніше загальні рівняння:
· прямої на площині Ax + By + C = 0, де 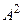 +
+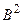
 0 та
0 та
· площини у просторі: Ax + By + Cz + D = 0, де 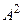 +
+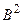 +
+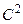
 0 є прикладами алгебраїчних рівнянь першого степеня.
0 є прикладами алгебраїчних рівнянь першого степеня.
Алгебраїчним рівнянням другого степеня називається рівняння вигляду:
A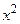 + Bxy + C
+ Bxy + C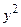 + Dx + Ey + F = 0, де
+ Dx + Ey + F = 0, де 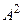 +
+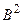 +
+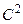
 0.
0.
Рівняння, яке рівносильне означеному, також називається алгебраїчним.
Задамо на площині декартову систему координат Oxy. Загальне рівняння лінії другого порядку переважно записують у вигляді:
A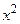 + 2Bxy + C
+ 2Bxy + C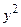 + 2Dx + 2Ey + F = 0,
+ 2Dx + 2Ey + F = 0,
де A, B, C, D, E, F – довільні числа, причому 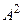 +
+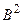 +
+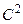
 0.
0.
При A = B = C = 0 отримуємо рівняння лінії першого порядку.
У загальному рівняння лінії другого порядку
A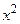 + 2Bxy + C + 2Bxy + C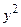 = Q(x, y) = Q(x, y)
| квадратична форма, |
| Dx + Ey = L(x; y) | лінійна форма. |
Таким чином, загальне рівняння другого порядку визначається сумою квадратичної форми, лінійної форми, та вільного члена:
Q(x, y) + 2L(x, y) + F = 0.
Якщо в загальному рівнянні коефіцієнт при добутку невідомих B = 0, то квадратична форма називається канонічною.
A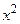 + C + C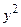 = = 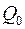 (x, y) (x, y)
| Канонічна квадратична форма |
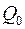 (x, y) + 2L(x, y) + F = 0 (x, y) + 2L(x, y) + F = 0
| Загальне рівняння з канонічною квадратичною формою |
Якщо у загальному рівнянні кривої крім коефіцієнта B дорівнюють нулю і коефіцієнти, які визначають лінійну форму, тобто L(x; y) = 0, то рівняння кривої називають канонічним.
A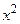 + C + C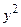 + F = 0 + F = 0
| Канонічне рівняння другого порядку |
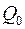 (x, y) + F = 0 (x, y) + F = 0
|
3. Етапи спрощення рівняння другого степеня. Перед спрощенням загального рівняння другого степеня з двома невідомими проведемо деякі узагальнення:
1. Загальне рівняння другого степеня описує в деякій системі координат на площині лінію другого порядку;
2. При переході до іншої системи координат лінія не змінює своєї форми (вона залишається такою самою і на цьому ж самому місці простору);
3. При переході до іншої системи координат змінюються значення коефіцієнтів алгебраїчного рівняння.
4. Перехід до іншої системи координат можна здійснити або за допомогою паралельного перенесення, або шляхом повороту осей координат на деякий кут j.
Переходом до іншої системи координат можна загальне рівняння лінії звести до більш простого (канонічного) вигляду.
Отже, нехай в системі координат лінія другого порядку описується загальним рівнянням другого степеня з двома невідомими:
A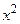 + 2Bxy + C
+ 2Bxy + C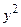 + 2Dx + 2Ey + F = 0.
+ 2Dx + 2Ey + F = 0.
Вважаючи, що всі коефіцієнти рівняння відмінні від нуля, зведемо загального рівняння до канонічного вигляду у два етапи:
- На першому етапі за допомогою перетворення звільняємось у рівнянні від коефіцієнта B, який знаходиться біля добутку змінних. У квадратичній формі наявність відмінного від нуля коефіцієнта при добутку двох невідомих (B 0) вказує на поворот кривої певного типу відносно координатних осей. Перетворення в нуль цього коефіцієнта може відбутись шляхом повороту осей координат на деякий кут j без переміщення початку координат. У новій системі координат квадратична форма загального рівняння лінії другого порядку буде канонічною.
0) вказує на поворот кривої певного типу відносно координатних осей. Перетворення в нуль цього коефіцієнта може відбутись шляхом повороту осей координат на деякий кут j без переміщення початку координат. У новій системі координат квадратична форма загального рівняння лінії другого порядку буде канонічною.
- На другому етапі перетворення звільняє загальне рівняння лінії другого порядку від лінійної форми L(x; y). Паралельне перенесення осей координат зануляє лінійну форму рівняння і зміщує систему координат у нове положення не повертаючи осей координат, внаслідок чого, загальне рівняння кривої другого порядку стає канонічним.
Перехід до канонічної форми. Нехай B 0. Тоді загальне рівняння кривої і її квадратична форма містять член з добутком біжучих координат x і y. Здійснимо перехід до нової системи координат
0. Тоді загальне рівняння кривої і її квадратична форма містять член з добутком біжучих координат x і y. Здійснимо перехід до нової системи координат  за формулами повороту осей на кут j відносно осей старої системи координат Oxy. Підстановка правих частин цих формул в загальне рівняння кривої другого порядку визначає рівняння:
за формулами повороту осей на кут j відносно осей старої системи координат Oxy. Підстановка правих частин цих формул в загальне рівняння кривої другого порядку визначає рівняння:
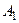
 + 2
+ 2
 +
+ 
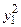 + 2
+ 2
 + 2
+ 2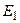
 +
+  = 0,
= 0,
де 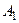 = A
= A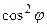 + Bsin2j + C
+ Bsin2j + C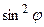 ,
,  =
=  sin2j + Bcos2j,
sin2j + Bcos2j,
 = A
= A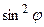 – Bsin2j + C
– Bsin2j + C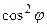 ,
,  = Dcosj + Esinj,
= Dcosj + Esinj,
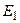 = – Dsinj + Ecosj,
= – Dsinj + Ecosj,  = F.
= F.
Умова  = 0 визначає кут повороту
= 0 визначає кут повороту  із рівнянь:
із рівнянь:
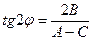 , якщо A
, якщо A C, і cosj = 0, якщо A = C.
C, і cosj = 0, якщо A = C.
За отриманим рівнянням знаходимо спочатку sin2j і cos2j, а потім sinj і cosj.
Підставляючи значення sinj і cosj у вирази для коефіцієнтів 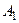 ,
,  ,
,  ,
,  ,
, 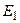 і
і  , отримаємо рівняння, яке не буде містити добутку невідомих.
, отримаємо рівняння, яке не буде містити добутку невідомих.
Отже, поворотом на кут j, який визначається через коефіцієнти квадратичної форми, здійснюється перехід від старої прямокутної декартової системи координат Oxy, в якій крива описувалась загальним рівнянням другого порядку
A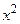 + 2Bxy + C
+ 2Bxy + C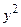 + 2Dx + 2Ey + F = 0,
+ 2Dx + 2Ey + F = 0,
до нової прямокутної системи координат  , осі якої повернуті відносно старих осей на знайдений кут в напрямку, протилежному до руху стрілки годинника. В новій системі координат в рівнянні кривої другого порядку є відсутнім добуток невідомих, тобто квадратична форма має канонічний вигляд:
, осі якої повернуті відносно старих осей на знайдений кут в напрямку, протилежному до руху стрілки годинника. В новій системі координат в рівнянні кривої другого порядку є відсутнім добуток невідомих, тобто квадратична форма має канонічний вигляд:
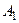
 +
+ 
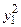 + 2
+ 2
 + 2
+ 2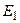
 +
+  = 0.
= 0.
Приклад 3. Спростити шляхом повороту осей координат рівняння кривої:
9 – 24xy + 16
– 24xy + 16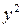 – 110x – 20y + 325 = 0.
– 110x – 20y + 325 = 0.
Розв’язування. В заданому рівнянні кривої
A = 9, B = –12, C = 16, D = –55, E = –10 і F = 325.
Знаходимо, на який кут слід повернути осі нової системи координат:
 , cos2j = 0,28, sinj =0,6, cosj = 0,8.
, cos2j = 0,28, sinj =0,6, cosj = 0,8.
Отже,  ,
,
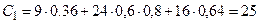 ,
,  ,
,
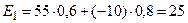 ,
, 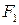 = 325.
= 325.
Таким чином, ми прийшли до рівняння:
25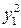 – 100
– 100 + 50
+ 50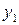 + 325 = 0 або
+ 325 = 0 або 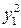 – 4
– 4 + 2
+ 2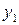 + 13 = 0.
+ 13 = 0.
Це рівняння параболи, яке шляхом паралельного перенесення початку координат в точку 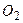 (3, –1) можна привести до канонічного вигляду.
(3, –1) можна привести до канонічного вигляду.
Перехід до канонічного рівняння. На цьому етапі перетворення рівняння будемо вважати, що зведення загального рівняння до канонічної форми вже здійснено, тобто зроблено поворот осей координат на кут j, B = 0 і загальне рівняння має вигляд:
A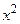 + C
+ C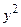 + 2Dx + 2Ey + F = 0.
+ 2Dx + 2Ey + F = 0.
У рівнянні квадратична форма має канонічний вигляд, але лінійна форма відмінна від нуля:
A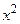 + C
+ C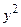 =
=  (x, y), L(x, y)
(x, y), L(x, y)  0.
0.
Щоб перейти до канонічного рівняння, необхідно здійснити паралельне перенесення осей координат в новий початок координат 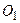 (a, b) за формулами:
(a, b) за формулами:

Підстановка в рівняння кривої значень x і y, приводить до рівняння:
A +C
+C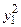 +2(Cb+D)
+2(Cb+D) +2(Cb+E)
+2(Cb+E) +A
+A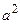 +C
+C +2(Da+Eb)+F = 0.
+2(Da+Eb)+F = 0.
Вибираючи a і b таким чином, щоб коефіцієнти при невідомих в першому степені дорівнювали нулю, отримуємо рівняння:
A +C
+C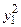 =
=  ,
,
де  ,
,  ,
, 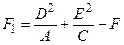 .
.
Таким чином, здійснюючи поворот системи координат на деякий кут j, і, здійснивши паралельне перенесення початку системи координат в нову точку  (a, b), будь-яке рівняння другого порядку можна звести до канонічного вигляду. При цьому в залежності від коефіцієнтів квадратичної канонічної форми отримуємо різні види кривих другого порядку.
(a, b), будь-яке рівняння другого порядку можна звести до канонічного вигляду. При цьому в залежності від коефіцієнтів квадратичної канонічної форми отримуємо різні види кривих другого порядку.
Приклад 4. Рівняння  +
+ 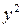 – 40x + 6y = 36 звести до канонічного.
– 40x + 6y = 36 звести до канонічного.
Розв’язування. У рівнянні лінії коефіцієнт при добутку невідомих дорівнює нулю, тому здійснимо перехід до нової системи координат 

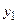 шляхом переносу початку координат у точку
шляхом переносу початку координат у точку 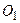 (a, b) за формулами:
(a, b) за формулами: 
.
Одержимо: 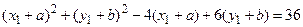 або спростивши:
або спростивши:
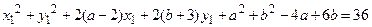 .
.
Вибором a = 2 і b = –3 зануляються коефіцієнти при  і
і 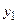 .
.
Отже, 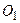 (2, –3), а підстановка a = 2 і b = –3 в рівняння переводить його до канонічного вигляду:
(2, –3), а підстановка a = 2 і b = –3 в рівняння переводить його до канонічного вигляду:  .
.
Це рівняння описує коло з радіусом R = 7 і центром в точці 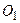 (2, –3).
(2, –3).

|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 2299; Нарушение авторских прав?; Мы поможем в написании вашей работы!