Тело кватернионов

Первой системой на пути обобщения комплексных чисел явились кватернионы, т. е. выражения вида , где а, b, с, d - действительные числа, а символы i, j, k также называют кватернионами. Число а - действи­тельная часть, а сумма - векторная часть кватер­ниона.

На множестве кватернионов определяют два внутренних закона. Аддитивный закон задается подобно сложению комплекс­ных чисел, т.е. сумма кватернионов 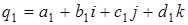и есть

.

Очевидно, этот закон ассоциативный и коммутативный. Нейтраль­ным элементом относительно сложения служит , а симметричным к элементу q есть элемент .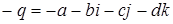

Чтобы множество кватернионов было телом, мультипликатив­ный закон (умножение кватернионов) должен быть ассоциативным и дистрибутивным относительно сложения. Это достигается, с одной стороны, определением мультипликативного закона подобно умно­жению многочленных алгебраических выражений и, с другой сто­роны, заданием правила умножения кватернионов, которое в наи­более лаконичной записи имеет вид:

,

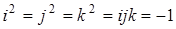где порядок сомножителей в произведении ijk строго фиксирован. Отсюда также следует

.

Действительно, умножая справа на k обе части равенства ijk = -1, имеем ijk² = - k или ij = k. Умножая полученное уравнение на j справа или на i слева, получаем соответственно - i = kj или - j = ik и т. д.

Геометрически умножение кватернионов легко представить с помощью диаграммы (рис. 7.2): произведение двух кватернионов равно третьему со знаком «+», если поворот от первого сомножителя ко второму осуществляется по часовой стрелке, и со знаком «-», если поворот против часовой стрелки.

Рис.7.2. Умножение кватернионов

Нетрудно проверить, что мультипликативный закон (умножение кватерни­онов) не коммутативный (проверяется непосредственным умножением с учетом изложенных выше правил). Нейтральным элементом относительно умножения служит еди­ница, рассматриваемая как кватернион, у которого а = 1 и b = с = d = 0. Можно также показать, что относительно умножения каждый кватернион имеет симметричный (обратный) ему

,

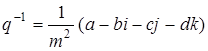где число 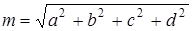называют нормой кватерниона. Итак, множество кватернионов, наделенное описанными выше двумя внутренними законами компо­зиции, образует тело.

В механике кватернионы применяются при решении задач, связанных с вращениями твердого тела в пространстве.

Дата добавления: 2014-01-13