
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Математические основы метода конечных элементов
|
|
|
|
Решение многих краевых задач для дифференциальных уравнений, в частности краевых задач механики, могут быть сведены к задаче нахождения min некоторого функционала 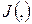 при соответствующих граничных условиях, для которого исходное дифф. уравнение является уравнением Эйлера-Лагранжа.
при соответствующих граничных условиях, для которого исходное дифф. уравнение является уравнением Эйлера-Лагранжа.
Пусть имеется краевая задача
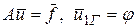 или другие граничные условия (1)
или другие граничные условия (1)
Если дифференциальный оператор А положительно определенный и самосопряженный, то соответствующая вариационная постановка для краевой задачи (1) имеет вид найти
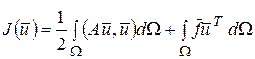 (2)
(2)
Вариационная задача имеет определенные преимущества по сравнению с постановкой (1): 1) порядок дифференциального оператора понижается в два раза; 2) возможность более удобного формулирования граничных условий, смягчение требований к координатным функциям; 3) возможность более простого представления разностных выражений.
Для задач механики (1) и (2) можно представить в виде
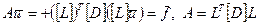 ,
, 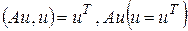 (1¢)
(1¢)
 матрица операции дифференцирования,
матрица операции дифференцирования, матрица свойств (упругости).
матрица свойств (упругости).
Найти 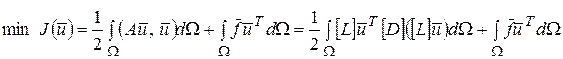 (2¢)
(2¢)
В терминах механики сплошных сред (2¢) можно представить в виде:




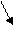


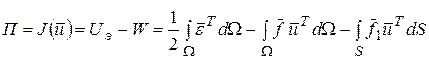 , (3)
, (3) 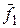
W

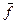
S
П - потенциальная энергия системы (тела); 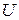 - потенциальная энергия деформации системы; W – работа (возможная) внешних сил;
- потенциальная энергия деформации системы; W – работа (возможная) внешних сил;  - тензор деформации;
- тензор деформации;  - вектор перемещений;
- вектор перемещений;  - матрица упругости; - матрица операций дифференцирования; Т – операция транспонирования матриц.
- матрица упругости; - матрица операций дифференцирования; Т – операция транспонирования матриц.
Для плоского случая 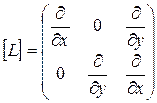 .
.
Для решения вариационной задачи (2), (2¢) или (3) можно применить прямые методы вариационного исчисления (метод Ритца, Бубнова- Галеркина т.д.). Основная трудность при непосредственном применении этих методов связана с выбором глобальных аппроксимирующих (базисных, координатных) функций для всей области. Эти функции должны не только удовлетворять главным граничным условиям, но и достаточно полно описывать геометрию, материал, другие характеристики задачи. С развитием ВТ получила развитие идея локализации аппроксимирующих функций (координатных) в малых областях (конечных элементах) и в 1950 годах возник метод конечных элементов в связи с решением задач космических исследований.
Основная идея метода конечных элементов состоит в том, что любую непрерывную величину можно аппроксимировать дискретной моделью, которая строится на множестве кусочно-непрерывных функций, определенных на конечном числе подобластей.
Математическая основа метода конечных элементов (МКЭ) – вариационное исчисление, т.е. нахождение 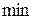 функционала. С этой точки зрения МКЭ представляет собой неявное применение метода Ритца на отдельных подобластях (конечных элементах).
функционала. С этой точки зрения МКЭ представляет собой неявное применение метода Ритца на отдельных подобластях (конечных элементах).
Основными этапами применения МКЭ являются следующие:
1) Дискретизация (разбиение) области (конструкции) на совокупность конечных элементов, взаимосвязанных в узловых точках.
2) Определение аппроксимирующих (координатных) функций для отдельных элементов (получение матриц элементов).
3) Получение из отдельных координатных функций элементов кусочно-непрерывной функции, определенной на всей области (учитываются граничные условия) минимизации функционала, связанного с физической задачей (строится общая матрица всей области).
4) Составление разрешающей системы уравнений путем минимизации функционала 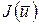 .
.
5) Решение полученной системы уравнений относительно узловых значений.
6) Вычисление искомых величин в элементах (других величин, связанных с определенной величиной - координатными функциями).
1. Дискретизация области на совокупность конечных элементов
Разбиение области на подобласти (КЭ) представляет собой первый шаг по пути к решению задачи, а именно этот шаг не имеет теоретического обоснования. Искусство разбиения области зависит от имеющихся навыков исследователя. Плохое разбиение будет приводить к ошибочным результатам, если даже остальные этапы МКЭ осуществляются достаточно точно.
Дискретизация области (тела) включает задание числа, размеров и формы подобластей (КЭ), которые используются для построения дискретной модели реального тела. Это очень деликатная ситуация. С одной стороны, элементы должны быть выбраны достаточно малыми, чтобы получились приемлемые результаты, а с другой стороны, применение достаточно крупных элементов сокращает вычислительную работу. В области больших величин градиентов размеры элементов уменьшены.
Используются элементы различных типов: а) одномерный элемент (схематически он отрезок, хотя может иметь поперечное сечение); б) двухмерные элементы (треугольники, четырехугольники); в) трехмерные элементы (тетраэдр, параллелепипед):

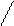
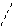













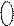
 а) б) в)
а) б) в)
 | ||||||||||
 |  |  |  | |||||||
 | ||||||||||








Процесс дискредитации может быть разделен на два этапа: разбиение тела на КЭ; б) нумерацию элементов и узлов.

















 а) Двумерные телаW обычно разбиваются на треугольные или четырехугольные элементы
а) Двумерные телаW обычно разбиваются на треугольные или четырехугольные элементы 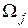 . Треугольные элементы – простейший из двумерных элементов в смысле аналитической формулировки задача и видимо это наилучший способ разбиения. При разбиении двумерной области сначала тело делится на треугольные и четырехугольные подобласти. Границы между подобластями должны проходить там, где изменяются геометрия, приложенная нагрузка или свойства материала. Например, разбиение четырехугольника с помощью короткой диагонали предпочтительно, потому что элементы, близкие по форме к равностороннему треугольнику, приводят к более точным результатам, чем длинные узкие треугольники.
. Треугольные элементы – простейший из двумерных элементов в смысле аналитической формулировки задача и видимо это наилучший способ разбиения. При разбиении двумерной области сначала тело делится на треугольные и четырехугольные подобласти. Границы между подобластями должны проходить там, где изменяются геометрия, приложенная нагрузка или свойства материала. Например, разбиение четырехугольника с помощью короткой диагонали предпочтительно, потому что элементы, близкие по форме к равностороннему треугольнику, приводят к более точным результатам, чем длинные узкие треугольники. 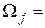















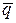 16 Р1
16 Р1


 23 26 21
23 26 21
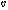









 9 14 23 27
9 14 23 27


















 6 10 11 22 21 24
6 10 11 22 21 24


 8 7 13 19
8 7 13 19



 6 5 14 20 Р2
6 5 14 20 Р2
5 4 16
4 12
3 3 15
 2
2
2 1 17 16
 20 Р3
20 Р3





 1 10 11
1 10 11
Рис.1.Напряженное состояние пластины с отверстием Рис.2.
б) МКЭ сводится к решению системы линейных алгебраических уравнений обычно с ленточной матрицей. Ширина полосы матрицы связана с требуемым объемом памяти ЭВМ и вычислений (уменьшение уменьшает объем). Минимизация величины  связана с минимизацией R – максимальной по элементам величины наибольшей разности между номерами узлов в отдельном элементе
связана с минимизацией R – максимальной по элементам величины наибольшей разности между номерами узлов в отдельном элементе 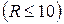 ; Q – число неизвестных (степеней свободы) в каждом узле. Поэтому, в частности, выгодна последовательная нумерация узлов при движении в направлении наименьшего размера тела. Нумерация элементов не влияет на вычислительные аспекты задачи.
; Q – число неизвестных (степеней свободы) в каждом узле. Поэтому, в частности, выгодна последовательная нумерация узлов при движении в направлении наименьшего размера тела. Нумерация элементов не влияет на вычислительные аспекты задачи.
П. Определение аппроксимирующих (координатных)
функций для отдельной КЭ 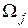
Согласно методу КЭ искомая непрерывная функция  аппроксимируется дискретной моделью, которая строится на множестве кусочно непрерывных функций, определенных на конечном числе подобластей (КЭ). Таким образом, вводятся функции
аппроксимируется дискретной моделью, которая строится на множестве кусочно непрерывных функций, определенных на конечном числе подобластей (КЭ). Таким образом, вводятся функции
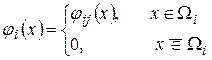
 , (4)
, (4)
где 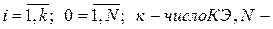 число узлов расчетной схемы (элемента). Тогда искомая функция для всей области
число узлов расчетной схемы (элемента). Тогда искомая функция для всей области 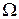 :
: 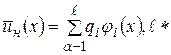 - общее число степеней свободы.
- общее число степеней свободы. 
 cтепени свободы
cтепени свободы 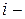 го узла.
го узла.
В качестве функций элементов чаще всего применяются полиномы.
 -число узлов
-число узлов 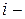 го КЭ.
го КЭ.
 Например, для одномерного симплекс-элемента (КЭ) и двумерного симплекса (КЭ)
Например, для одномерного симплекс-элемента (КЭ) и двумерного симплекса (КЭ)

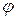
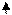
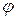
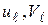











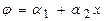
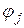












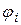
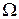

 |








 i j x y
i j x y




 xi
xi





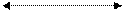

 xj (
xj (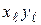 ) Wi m (
) Wi m ( )
)






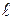 n
n
x ( )
)
Можно использовать аппроксимирующие полиномы более высокого порядка (нелинейные). Далее значения искомой функции  в любой точке внутри элемента можно выразить через его значения в узлах и его координатах.
в любой точке внутри элемента можно выразить через его значения в узлах и его координатах.
Пусть 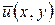 =
= и (5.1) (5)
и (5.1) (5)
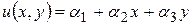 (5.2)
(5.2) 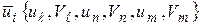 ,
,
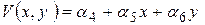 (5.3)
(5.3)
В узлах КЭ выполняются следующие условия:
 или
или 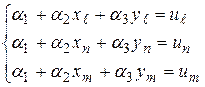 (6)
(6)
или в матричной форме
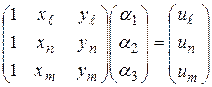 . (6¢)
. (6¢)

После определения коэффициентов  из системы (6) и подстановки их в равенство (5.2) получим выражения для
из системы (6) и подстановки их в равенство (5.2) получим выражения для 

= , (7)
, (7)
где 

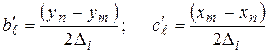 (8.1)
(8.1)
Остальные коэффициенты 
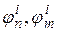 получаются из (8.1) с помощью круговой перестановки индексов
получаются из (8.1) с помощью круговой перестановки индексов 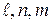 , т.е.
, т.е.
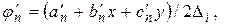

(8.2)
 ,
, 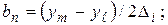

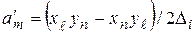 ;
;  ;
;
 ; (8.3)
; (8.3)
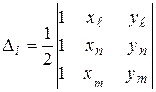 площадь
площадь 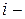 го треугольного КЭ. Причем,
го треугольного КЭ. Причем,  .
.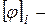 матрица функции формы
матрица функции формы 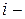 го КЭ,
го КЭ,
 - узловые перемещения
- узловые перемещения 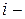 го КЭ.
го КЭ.
Аналогично определяются  для (5.3)
для (5.3)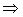
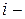 го
го
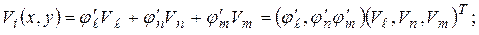 (7.3)
(7.3) 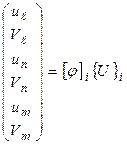
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 1049; Нарушение авторских прав?; Мы поможем в написании вашей работы!