Вопрос 2. Взаимное расположение двух точек

Вопрос 1. Позиционные задачи

Тема: Задачи на взаимную принадлежность точек, прямых и плоскостей

ПЛАН-КОНСПЕКТ (ТЕЗИСЫ ЛЕКЦИИ) №9

Учебные и воспитательные цели: рассмотреть, какое место занимает проекционное черчение для умения читать и разрабатывать чертежи изделий, изучить способы проецирования, рассмотреть основные вопросы, связанные с комплексными чертежами точки, прямой, плоскости.

Учебные вопросы	Время, мин.
Вступительная часть
1. Позиционные задачи
2. Взаимное расположение двух точек
3. Взаимное расположение точек и прямой
4. Взаимное расположение двух прямых
5. Взаимное расположение точки и плоскости
Заключительная часть

Литература

1. Фазлулин, Э. М., Инженерная графика: учебник / Э. М. Фазлулин, В. А. Халдинов – М., 2009.

2. Чекмарев, А. А. Инженерная графика: Учеб. для немаш. спец. вузов. / А. А. Чекмарев. – М: Высш. шк., 2009.

Позиционными называют задачи, в которых определяется взаимное расположение различных геометрических фигур.

К таким задачам относятся задачи на взаимопринадлежность (построение точки на линии или поверхности, проведение линии на поверхности или поверхности через заданные линии и другие) и задачи на пересечение (пересечение линии с плоскостью и поверхностью, пересечение плоскости с плоскостью и поверхностью, пересечение поверхностей).

Различают «прямые» и «обратные» позиционные задачи. В прямых задачах необходимо построить чертежи оригиналов, расположенных определенным образом относительно друг друга. В обратных позиционных задачах по имеющемуся чертежу определяется взаимное расположение точек, прямых и плоскостей относительно друг друга.

Возможно всего два варианта расположения двух точек в пространстве: точки совпадают или не совпадают. Если две точки совпадают, то совпадают и все их проекции (рисунок 1,а).

Когда точки не совпадают в пространстве, то их проекции могут:

1) не совпадать на всех проекциях (рисунок 1, б);

2) не совпадать хотя бы на одной проекции (рисунки 1, в, г).

При несовпадении точек в пространстве возникает вопрос: как они расположены относительно друг друга?

Рассматривая чертеж (рисунок 1, б), определяем, что точка А расположена левее точки В на величину a, ближе точки В на величину b и ниже точки В на величину c.

На рисунке 1, в и 1, г изображены, соответственно, горизонтально конкурирующие точки C=D и фронтально конкурирующие точки E=F.

Как видно, точка C выше точки D на величину d, а точка E ближе точки F на величину e.

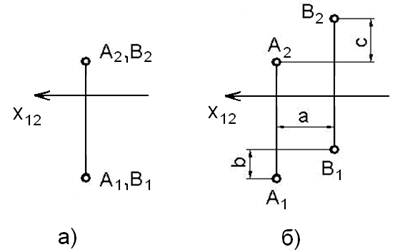
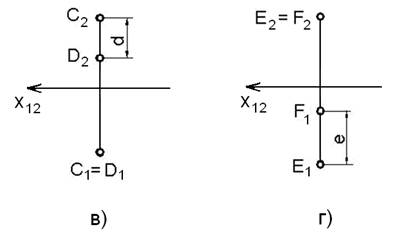
Рисунок 1 – Взаимное расположение двух точек (продолжение)

Дата добавления: 2014-01-13