Высказывание

ОСНОВНЫЕ ПОНЯТИЯ АЛГЕБРЫ ЛОГИКИ

План:

1. Высказывание;

2. Конъюнкция (логическое «И») – логическое умножение;

3. Дизъюнкция (логическое «ИЛИ») - логическое сложение

4. Импликация – логическое следование

5. Эквивалентность – логическое равенство

6. Отрицание (НЕ) – инверсия

7. Сложение по модулю 2

8. Основные законы алгебры логики

9. Условные обозначения логических элементов

Одним из исходных, неопределяемых понятий математической логики является высказывание.

Высказывание - это повествовательное предложение, относительно которого можно говорить, истинно оно или ложно. Повествовательное предложение можно записать на обычном языке, на специальных языках математики, химии, физики и т. д. Приведем примеры высказываний.

1) 2³=8.

2) Минск - столица Беларуси.

3) Волга впадает в Черное море.

Первые два высказывания являются истинными, а третье - ложным. Подчеркнем, что вопросительные, восклицательные, побудительные предложения, а также определения не являются высказываниями. Более того, не всякое повествовательное предложение является высказыванием. Так, нельзя считать высказыванием следующие предложения.

1) Тюльпаны самые красивые цветы.

2) Студенты-математики - самые трудолюбивые.

3) Х+5>10.

В самом деле, разным людям нравятся разные цветы и именно их они считают самыми красивыми, поэтому не может быть единого мнения о самых красивых цветах. Истинность третьего предложения также нельзя определить, так как неизвестно, о каком Х идет речь. В математической логике интересуются только истинностью или ложностью высказывания, а не его содержанием (смыслом).

Всякое высказывание является либо истинным, либо ложным и не может быть и истинным, и ложным одновременно. Значения, которые могут принимать высказывания,- истина, ложь - обозначают соответственно И, Л или цифрами 1, 0. В англоязычной литературе используются обозначения True - истина, False - ложь.

Сложные высказывания. Из исходных элементарных высказываний с помощью слов "не", "и", "или", "если…, то", "тогда и только тогда, когда..." можно строить сложные высказывания. Приведенные слова называют логическими связками. Другими словами, над элементарными высказываниями можно выполнять логические операции.

2. Конъюнкция (логическое «И») – логическое умножение

Конъюнкцией (conjunctio - соединение, союз, связь) высказываний А и В называется сложное высказывание "А и В", которое истинно тогда и только тогда, когда А и В одновременно истинны.

Операция конъюнкции обозначается: А∩B; А&В; А*В; А and В; А И В.

Таблица истинности

А	B	A L B

Пересечение множеств

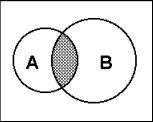
А - множество отличников в классе В - множество спортсменов в классе А L В - множество отличников, занимающихся спортом

Пример. А: 2³=8, В: Минск - столица Беларуси. Тогда конъюнкция А∩B истинна, поскольку А и В одновременно истинны.

3. Дизъюнкция (логическое «ИЛИ») -логическое сложение

Дизъюнкцией (disjunctio - разделение, различие) высказываний А и В называют сложное высказывание "А или В", которое ложно тогда и только тогда, когда А и В одновременно ложны.

Обозначается:

А или В; А OR В; А + В; А V В

Таблица истинности

А	B	A V B

Объединение множеств

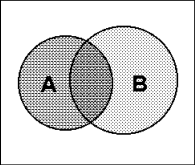
А - множество отличников в классе В - множество спортсменов в классе А È В - множество учеников класса, которые являются отличниками или спортсменами

4. Импликация – логическое следование

Импликацией (implicatio - тесно связанное, сплетенное) высказываний А и В называется сложное высказывание "если А, то В", которое ложно тогда и только тогда, когда А истинно, а В - ложно. Импликацию двух высказываний будем обозначать как А => В. Часто в математике А называют посылкой (условием), а В называют следствием (заключением). Таблица истинности для операции импликации имеет вид:

А	B	A Þ B	Пояснение	“Если идет дождь, то асфальт мокрый”
			дождя нет, асфальт сухой	ИСТИНА
			дождя нет, асфальт мокрый	ИСТИНА
			дождь идёт, асфальт сухой	ЛОЖЬ
			дождь идёт, асфальт мокрый	ИСТИНА

5. Эквивалентность – логическое равенство

Эквивалентностью двух элементарных высказываний А и В называют сложное высказывание "А тогда и только тогда, когда В", которое истинно только тогда, когда оба высказывания А, В принимают одинаковое значение истинности.

Эквивалентность обозначается: А <=> В, А Eq В, А = В; А ~ В

В математике А <=> В читается как "А тогда и только тогда, когда В", "А эквивалентно В", "А необходимо и достаточно для В".

А	B	A Û B	Пояснение	“Число кратно трём тогда и только тогда, когда сумма цифр кратна трём”
			число не кратно трём, сумма цифр не кратна трём	ИСТИНА
			число не кратно трём, сумма цифр кратна трём	ЛОЖЬ
			число кратно трём, сумма цифр не кратна трём	ЛОЖЬ
			число кратно трём, сумма цифр кратна трём	ИСТИНА

6. Отрицание (НЕ) – инверсия

Инверсия (от лат. inversio - переворачивание)

Отрицанием высказывания А называют высказывание "не А", которое истинно, когда А ложно, и ложно, когда А истинно.

Инверсия обозначается: не А; ¬А; not A,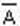

Отрицание высказывания А можно определить с помощью таблицы истинности, которая имеет вид:

A

Из таблицы следует, что если А - истинно (А = 1), то - ложно ( = О), и наоборот.

Таблица истинности ИЛИ-НЕ, И-НЕ

Входные переменные	ИЛИ y = x1+x2	И y = x1x2	ИЛИ-НЕ	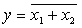И-НЕ
x1	x2
0 0 1 1	0 1 0 1	0 1 1 1	0 0 0 1	1 0 0 0	1 1 1 0

Вычисление значений логических выражений выполняется в определенном порядке, согласно их приоритету:

- инверсия

- конъюнкция

- дизъюнкция

- импликация и эквивалентность

Операции одного приоритета выполняются слева направо. Для изменения порядка действий используются скобки.

Дата добавления: 2014-01-13