
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Общий вид системы линейных алгебраических уравнений (СЛАУ). Понятие о прямых методах решения СЛАУ
|
|
|
|
Алгебраических уравнений
Прямые методы решения систем линейных
ОСНОВЫ ЧИСЛЕННЫХ МЕТОДОВ
Лекция-2
Основная запись СЛАУ. Понятие решения СЛАУ и некоторые определения. В общем случае основная запись системы n линейных алгебраических уравнений с n неизвестными имеет следующий вид:
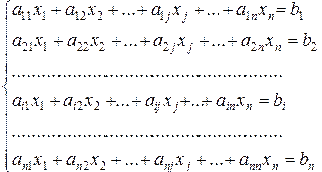 (2.2.1)
(2.2.1)
При этом через 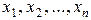 обозначены неизвестные, подлежащие определению; величины
обозначены неизвестные, подлежащие определению; величины 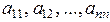 называемые коэффициентами системы, и величины
называемые коэффициентами системы, и величины 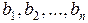 , называемые свободными членами, предполагаются известными. Каждый коэффициент системы
, называемые свободными членами, предполагаются известными. Каждый коэффициент системы 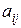 имеет два индекса, первый из которых
имеет два индекса, первый из которых 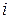 указывает номер уравнения, а второй
указывает номер уравнения, а второй 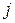 номер неизвестного, при котором стоит этот коэффициент.
номер неизвестного, при котором стоит этот коэффициент.
Система (2.2.1) называется однородной, если все ее свободные члены 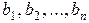 равны нулю.
равны нулю.
Если хотя бы один из свободных членов 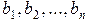 отличен от нуля, то система (2.2.1) называется неоднородной.
отличен от нуля, то система (2.2.1) называется неоднородной.
Решением системы (2.2.1) называется такая совокупность 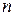 чисел
чисел 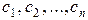 , которая при подстановке в систему (2.2.1) на место неизвестных
, которая при подстановке в систему (2.2.1) на место неизвестных 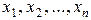 обращает все уравнения этой системы в тождества.
обращает все уравнения этой системы в тождества.
Система уравнений вида (2.2.1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее не существует ни одного решения.
Совместная система вида (2.2.1) называется определенной, если она имеет единственное решение.
Совместная система вида (2.2.1) называется неопределенной, если у нее существуют по крайней мере два различных решения.
Краткая запись СЛАУ:
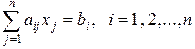 . (2.2.2)
. (2.2.2)
Матричная формулировка СЛАУ:
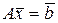 , (2.2.3)
, (2.2.3)
где
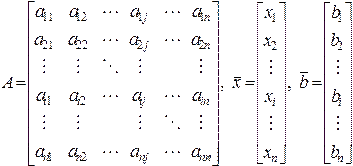 ; (2.2.4)
; (2.2.4)
 – матрица коэффициентов системы;
– матрица коэффициентов системы; 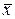 – вектор неизвестных;
– вектор неизвестных;  – вектор свободных членов.
– вектор свободных членов.
Представление с помощью расширенной матрицы. В действительности, система уравнений полностью определяется элементами матрицы и вектора правой части. Обозначения неизвестных имеют чисто символический смысл. При различных допустимых преобразованиях системы также меняются только значения элементов матрицы и правой части. Поэтому вполне достаточным представлением системы уравнений является, так называемая, расширенная матрица (она получается из матрицы коэффициентов системы путем добавления к этой матрице столбца свободных членов):
 (2.2.5)
(2.2.5)
где 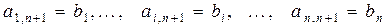 .
.
Прямые методами решения СЛАУ называются методы, которые позволяют получить теоретически точное (с учетом ограниченности разрядной сетки ЭВМ) решение за конечное число операций. Прямым методом является, в частности, метод Гаусса,
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 1471; Нарушение авторских прав?; Мы поможем в написании вашей работы!