Модели источников

Чем меньше вероятность появления знака, тем больше количество информации в нем содержится, тем он ценнее.

В самом деле, если учесть, что количество информации, содержащейся в одном любом знаке:

I(a_i)=-log₂h(a_i), (бит/знак)

то нетрудно видеть, что число двоичных посылок, содержащейся в знаке a_iс вероятностью р(a_i)=1/16больше (в 4 раза), чем в знаке а_j с р(а_j)=1/2 потому что I(a_i)=-log₂1/16=4 бита, а I(a_j) =-log₂1/2=14 бит

Чем большая взаимозависимость знаков, тем меньшее количество информации несет сообщение, составленное из них.

Пример: в английских текстах вслед за буквой q всегда идет u(т.е. qu). Если не учитывать эту взаимозависимость, то количество информации, заключенное о данных двух буквах будет:

I(qu)=-[log₂h(q)+log₂(u)]=-(log1/32+log1/32)=5+5=10 бит

Если же учитывать, то передавать следует по каналу связи только первую букву, а вторую бессмысленно (ведь абсолютно известно, что за q последует только u, а передача известного не несет, по теории связи, никакой информации, тогда)

I(qu)=5 бит

Деления источников по стабильности вероятностей появления знаков a_i на выходе источников. Они делятся на 4 типа:

· нестационарные

· стационарные

· эргодические

· детерминированные

1. Источники для которых р(a_i) резко меняются во времени.

Примером такого рода источников может служить дискретный источник, знаками которого являются спортсмены на олимпийских играх. Вероятность победы каждого на данных играх одна (в зависимость от степени подготовки), но на следующих играх (через 4 года) она будет другая, а через 8 лет вообще будет отличаться.

2. Стационарные составляют источники, вероятность появления знаков которых слабо меняется во времени (практически не меняется)

3. Эргодические образуют источники, вероятность появления знаков которых оказывается одними и теми же. Стационарные и эргодические источники объединяют почти все реальные источники, например, состоящие из буквенных текстов (телеграф, телефон и др.). Мы будем заниматься только эргодическими.

4. Детерминированные с стопроцентными известными вероятностными характеристиками. При этом взаимозависимости их знаков найдена (рассчитана): она известна до появления едва ли не бесконечного по счету знака, следующего за данным.

Примером их могут служить движения небесных объектов (планет, звезд, галактик и т.д.) здесь вес известно (их траектория) на тысячелетия вперед.

Второе деление:

· с равновероятными независимыми знаками

· с неравновероятными независимыми знаками

· с неравновероятными зависимыми знаками

это источники, для которых вероятности появления каждого знака (на выходе источника сообщений) равны друг другу.

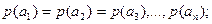
и нет взаимозависимости знаков

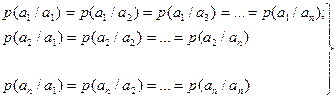
Для таких источников количество информации заключенное в одном любом знаке, одинаковы:

Здесь количество информации, заключенное в одном любом знаке, совпадает с энтропией.

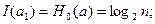
Такие источники нереальные (в периоде появления знаков источников информации).

Источники информации с независимыми неравновероятными знаками:

Вероятности появления знаков не равны между собой:

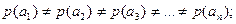
и нет взаимозависимости знаков:

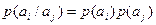
Количество информации:

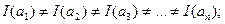
Энтропия:

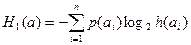
Энтропия здесь меньше, чем в первой модели. Энтропия определяет неопределенность ситуации. Если известно, какой знак будет выдан в данное мгновение (это в первой модели), энтропия будет максимальной. Если же абсолютно известно сообщений (вероятность равна единице) – энтропия равна нулю, р(а_i)=1, Н₁(а)=0.

т.е. для определения первой модели было ничего неизвестного, для второго что – то пояснялось, поэтому энтропия для второй модели будет лежать в пределах:

Н₀(а)> Н₁(а)>0

Источники с неравновероятными зависимыми знаками.

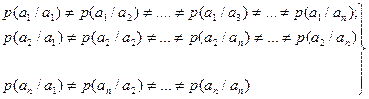
взаимозависимость:

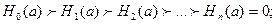
Дата добавления: 2014-01-13