Принцип суперпозиции состояний

Итак, непосредственный физический смысл связывается не с самой функцией ψ, а с квадратом ее модуля ψψ^*. Возникает вопрос: почему же в квантовой механике рассматривается сама волновая функция ψ, а не непосредственно наблюдаемая на опыте ψψ^*? Это необходимо для истолкования свойств вещества – интерференции и дифракции, которые отражают объективные, реально наблюдаемые волновые свойства материи. Здесь дело обстоит точно так же, как и во всей волновой теории. Эта теория принимает справедливость принципа суперпозиции самих волновых полей, а не их интенсивностей, пропорциональных квадрату полей, что позволяет включать в теорию явления интерференции и дифракции. Так и в квантовой механике принимается в качестве одного из основных постулатов принцип суперпозиции волновых функций. Оправданием такого принципа является согласие с опытом вытекающих из данного принципа следствий. Суть данного принципа заключается в следующем. Если ψ₁ и ψ₂ – какие-либо два решения уравнения Шрёдингера, то и всякая линейная их комбинация α₁ψ₁ + α₂ψ₂ с постоянными и в общем случае комплексными коэффициентами α₁ и α₂ также является решением уравнения Шрёдингера.

Во-вторых, если волновые функции ψ₁ и ψ₂ описывают какие-либо два состояния системы, то и линейная их комбинация α₁ψ₁ + α₂ψ₂ также описывает какое-то состояние этой системы.

Рассмотрим некоторую физическую величину f, характеризующую состояние квантовой системы. Значения, которые может принимать данная физическая величина, называют в квантовой механике ее собственными значениями, а об их совокупности говорят как о спектре собственных значений данной величины.

В квантовой механике, как и в классической, существуют физические величины (например координаты), собственные значении которых заполняют непрерывный ряд. Тогда говорят о непрерывном спектре собственных значений. Наряду с такими величинами в квантовой механике существуют величины, собственные значения которых образуют некоторый дискретный набор; в таких случаях говорят о дискретном спектре. Пусть рассматриваемая величина f обладает дискретным спектром, и ее собственные значения обозначим как f_n = (n – 0, 1, 2, 3, …). Обозначим волновую функцию системы в состоянии, в котором величина f имеет значение f_n, как ψ _n – cобственные функции величины f. Каждая из этих функций предполагается нормированной:

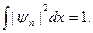(1)

Если система находится в некотором произвольном состоянии с волновой функцией ψ, то произведенное над ней измерение величины f даст одно из собственных значений f_n. В соответствии с принципом суперпозиции волновую функцию произвольного состояния можно представить в виде ряда

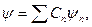(2)

где С_n – некоторые не зависящие от координат коэффициенты (для состояний, изменяющихся со временем, коэффициенты С_n зависят от времени). Последнее соотношение означает, что всякая волновая функция может быть разложена по собственным функциям любой физической величины. В квантовой механике доказывается, что квадрат модуля | C_n |² каждого из коэффициентов разложения (1) определяет вероятность соответствующего значения f_n величины в состоянии с волновой функцией ψ. Сумма вероятностей всех возможных значений f_n, очевидно, должна быть равна единице:

(3)

(если бы функция ψ не была нормированной, то не имело бы места и соотношение (3)).

Кроме того, сами коэффициента ряда (2) могут быть найдены по формуле

(4)

С учетом разложения (2) можно увидеть, что собственные функции должны удовлетворять условиям

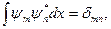(5)

где δ_nm = 1 при n = m и δ_nm = 0 при n ≠ m. Если говорить точно, то условие (5) выполняется только для невырожденного спектра энергии. Спектр считается невырожденным, если каждому значению энергии соответствует волновая функция.

Функции, подчиняющиеся условию (5), называются ортогональными. Таким образом, совокупность собственных функций ψ_n образует полную систему нормированных и взаимно ортогональных функций, или как говорят для краткости, систему ортонормированных функций.

Дата добавления: 2014-01-11