
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теоремы теории игр для парных матричных игр с нулевой суммой
|
|
|
|
Основные теоремы двойственности и их экономическое содержание
Теоремы двойственности позволяют установить взаимосвязь между оптимальными решениями пары двойственных задач. Решив одну из пары двойственных задач, можно или найти оптимальное решение другой задачи, не решая ее, или установить его отсутствие. Возможны следующие случаи:
1) обе задачи из пары двойственных задач имеют оптимальные решения;
2) одна из задач не имеет решения ввиду неограниченности целевой функции, а другая – ввиду несовместности системы ограничений.
Теорема 5.1. (Основное неравенство теории двойственности)Для всех допустимых планов x и y пары взаимно двойственных задач справедливо неравенство F (x) ≤ Z (y).
Его экономическое содержание состоит в том, что для любого допустимого плана производства x и любого допустимого вектора оценок ресурсов y, общая созданная стоимость не превосходит суммарной оценки ресурсов.
Теорема 5.2. (Достаточный признак оптимальности) Если для некоторых допустимых планов x* и y* пары двойственных задач выполняется равенство F (x*) =Z (y*), то x* и y* являются оптимальными планами соответствующих задач.
Экономический смысл критерия: план производства x и вектор оценок ресурсов y являются оптимальными, если цена всей произведенной продукции и суммарная оценка ресурсов совпадают.
Теорема 5.3. (Существование оптимальных планов пары двойственных задач) Для существования оптимального плана каждой из пары двойственных задач необходимо и достаточно существование допустимого плана для любой из них.
Теорема 5.4. Если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем экстремальные значения целевых функций совпадают, то есть F (x*) =Z (y*). Если одна из двойственных задач неразрешима, вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива.
Экономическое содержание теоремы:если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения оценок ресурсов, причем цена продукта полученного в результате реализации оптимального плана совпадает с суммарной оценкой ресурсов.
Связь между задачами двойственной пары глубже, чем указано в формулировке теоремы: решая симплекс-методом одну из них, автоматически получаем решение другой. Для этого достаточно воспользоваться соответствием переменных прямой и двойственной задач и оценок в последней симплекс-таблице:

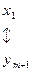


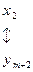

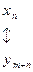
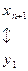


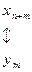 .
.
Теорема 5.5. Двойственная задача к двойственной есть прямая задача.
Теорема 5.6. Если пара двойственных задач имеет оптимальное решение, то при этом оптимальное значение переменных прямой задачи равно симплекс-множителям оптимального решения двойственной задачи, а значение переменных оптимального решения двойственной задачи равно симплекс-множителям оптимального решения прямой задачи.
Педагогический комментарий. Данное лекционное занятие закладывает основы для формирования следующих профессиональных умений студентов-экономистов: умение выявлять проблемы экономического характера при анализе конкретных ситуаций, предлагать способы их решения и оценивать ожидаемые результаты; умение разрабатывать и обосновывать варианты эффективных производственно-технологических решений; умение ставить цель и формулировать задачи, связанные с профессиональной деятельностью, умение использовать для их решения методы изученных дисциплин; умение логически мыслить; умение совершенствовать составление оперативно-производственного плана с использованием инструментария математического программирования; умение эффективно управлять экономическими процессами и регулировать использование комплекса имеющихся ресурсов; умение определять меру дефицитности ресурсов и оценку рентабельности или убыточности производимой продукции.
Тема 5. Элементы теории матричных игр
План лекции:
1. Основные понятия
2. Теоремы теории игр для парных матричных игр с нулевой суммой
3. Способы решения задач теории игр (ТИ)
1.Основные понятия
В ТИ рассматриваются ситуации связанные с принятием решений, в которых два лица, принимающих решение, имеют конфликтующие цели. К числу типичных примеров относится рекламирование конкурирующих товаров и планирование военных стратегий противоборствующих армий.
Каждый из двух участников игрового конфликта, именуемый игроком, имеет некоторое множество (конечное или бесконечное) возможных выборов решения, которые называются стратегиями. Такие игры известны как парные игры с нулевой суммой, так как выигрыш одного игрока равен проигрышу другого.
При обозначении игроков через А и В с числом стратегий m и n соответственно игру обычно представляют в виде матрицы платежей игроку А:
A= 


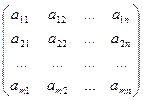
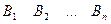
Такое представление матричной игры означает, что если игрок А использует стратегию i, а игрок В – j, то платеж игроку А составляет 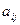 .
.
Определение 6.1. Ходом в игре называется принятие игроком на каждом ситуационном этапе определенного решения и выполнение на его основании действий, направленных на достижение поставленной этим игроком цели. Все допустимые альтернативные варианты хода игрока – стратегии.
Различают чистые и смешанные стратегии. Если очередной ход предписывается игроку однозначно (то есть вероятность осуществления такого хода равна 1), то стратегия называется чистой. Если же рекомендуется сделать ход с предписываемой вероятностью (0 < p < 1), то стратегия называется смешанной. Чистая стратегия, входящая в смешанную с ненулевой вероятностью, называется активной стратегией. Стратегия игрока называется оптимальной, если при многократном повторении игры она обеспечивает ему максимально гарантированный средний выигрыш или минимальный средний проигрыш.
Последовательность осуществленных ходов от начала игры до ее исхода называется партией игры.
Найти решение игры значит определить оптимальные стратегии игроков и цену игры, при этом первый игрок стремится обеспечить себе наибольший выигрыш, а второй – наименьший проигрыш.
Рассмотрим игру со следующей матрицей платежа:
А= 
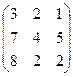
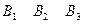
Определение 6.2. Нижней ценой игры (максимином) называется число 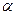 , определяемое по формуле:
, определяемое по формуле:
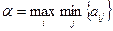 .
.
Для указанной матрицы 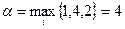 .
.
Определение 6.3. Верхней ценой игры (минимаксом) называется число 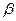 определяемое по формуле:
определяемое по формуле:
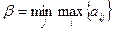 .
.
Для указанной матрицы 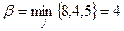 .
.
Стратегии игроков, соответствующие максимину (минимаксу), называются максиминными (минимаксными). Сумма выигрыша называется ценой игры и обозначается с.
В рассмотренной игре 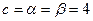 , что соответствует элементу матрицы
, что соответствует элементу матрицы 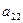 . Элемент матрицы А,определяющий цену игры, называется седловой точкой, а сама игра – игрой с седловой точкой. В игре с седловой точкой оптимальное решение для каждого игрока – чистая стратегия. Решением рассмотренной задачи является
. Элемент матрицы А,определяющий цену игры, называется седловой точкой, а сама игра – игрой с седловой точкой. В игре с седловой точкой оптимальное решение для каждого игрока – чистая стратегия. Решением рассмотренной задачи является 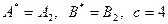 .
.
Теорема 6.1. (Основная теорема ТИ) Всякая конечная игра имеет цену, и у каждого игрока существует, по крайней мере, одна оптимальная стратегия.
Теорема 6.2. В матричной игре нижняя цена игры не превосходит верхней цены игры, то есть 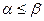 , а для цены игры с справедливо: a £ с £ b.
, а для цены игры с справедливо: a £ с £ b.
Определение 6.4. Смешанной стратегией первого (второго) игрока называется вектор 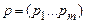 , где
, где 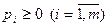 и
и 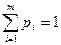 , (
, ( , где
, где 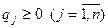 и
и  ).
).
Теорема 6.3. Игра с седловой точкой имеет оптимальное решение в чистых стратегиях.
Теорема 6.4. (Теорема Неймана ) Всякая матричная игра с нулевой суммой имеет решение в смешанных стратегиях, если чистую стратегию считать частным случаем смешанной, когда одна вероятностная компонента равна 1, а остальные – нулю.
Теорема 6.5. Для того чтобы смешанные стратегии 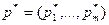 и
и 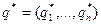 были оптимальными для игроков А и В в игре с платежной матрицей
были оптимальными для игроков А и В в игре с платежной матрицей  и выигрышем с, необходимо и достаточно выполнение неравенств:
и выигрышем с, необходимо и достаточно выполнение неравенств:
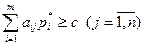 – сложение по столбцу,
– сложение по столбцу,
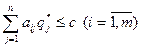 – сложение по строке.
– сложение по строке.
То есть первый игрок, придерживаясь своей оптимальной стратегии  , не может выиграть меньше с, второй игрок, придерживаясь своей оптимальной стратегии
, не может выиграть меньше с, второй игрок, придерживаясь своей оптимальной стратегии 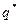 , не позволит первому выиграть больше с.
, не позволит первому выиграть больше с.
Данная теорема дает ответ на вопрос о существовании решения игры и определяет путь решения.
Теорема 6.6. (Об активных стратегиях) Если игроки придерживаются своих активных стратегий, то выполняется следующая система уравнений:
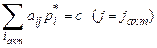 – сложение по столбцу активной стратегии,
– сложение по столбцу активной стратегии,
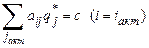 – сложение по строке активной стратегии.
– сложение по строке активной стратегии.
Теорема 6.7. Оптимальные смешанные стратегии  и
и 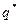 соответственно игроков А и В в матричной игре с платежной матрицей
соответственно игроков А и В в матричной игре с платежной матрицей  с ценой с будут оптимальными и в матричной игре с платежной матрицей
с ценой с будут оптимальными и в матричной игре с платежной матрицей 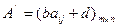 с ценой игры
с ценой игры 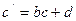 , где b> 0.
, где b> 0.
3. Способы решения задач ТИ:
1)Простейшими из матричных игр являются игры 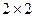 ,
, 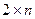 и
и 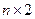 . Использование теоремы 6.6 для таких игр составляет первый способ решения.
. Использование теоремы 6.6 для таких игр составляет первый способ решения.
Пример 1. Найти решение игры, заданной матрицей:
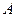
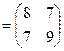 .
.
Решение:
1) Найдем нижнюю и верхнюю цену игры:
 ,
,
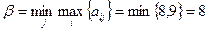 .
.
Следовательно, 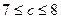 . Так как
. Так как 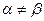 , то игра не является игрой с седловой точкой и решение следует искать в смешанных стратегиях.
, то игра не является игрой с седловой точкой и решение следует искать в смешанных стратегиях.
2) Пусть 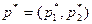 и
и  – оптимальные смешанные стратегии первого и второго игроков соответственно. Тогда по теореме 6.6 получим системы:
– оптимальные смешанные стратегии первого и второго игроков соответственно. Тогда по теореме 6.6 получим системы:
 и
и 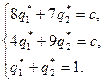
Решим первую систему. Вычитая из первого второе уравнение системы, получим  или
или 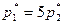 . Подставив это соотношение в третье уравнение, будем иметь
. Подставив это соотношение в третье уравнение, будем иметь 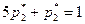 , откуда
, откуда 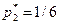 . Следовательно,
. Следовательно,  . Цену игры можно найти, если подставить полученные значения
. Цену игры можно найти, если подставить полученные значения 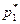 и
и 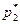 в одно из первых уравнений системы. Так, согласно первому уравнению
в одно из первых уравнений системы. Так, согласно первому уравнению 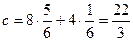 .
.
Аналогично получаем решение второй системы:
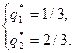
Ответ: 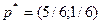 ,
, 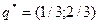 , с= 22/3.
, с= 22/3.
2)Графический способ решения матричных игр 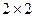 ,
, 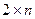 и
и 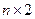 .
.
Пример 2. Найти решение игры, заданной матрицей:
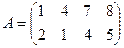 .
.
Решение:
1) Найдем нижнюю и верхнюю цену игры:
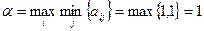 ,
,
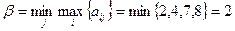 .
.
Следовательно, 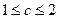 .
.
2) Изобразим стратегии игроков на плоскости pОq (рис. 6.1). Горизонтальной выбирается та ось, которая соответствует игроку с двумя стратегиями. На горизонтальной оси Оp выбирается отрезок 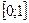 . Из точек 0 и 1 восстановим перпендикуляры и на них отложим выигрыши первого игрока при использовании вторым игроком своих возможных стратегий. Соединим соответствующие точки на перпендикулярах прямыми:
. Из точек 0 и 1 восстановим перпендикуляры и на них отложим выигрыши первого игрока при использовании вторым игроком своих возможных стратегий. Соединим соответствующие точки на перпендикулярах прямыми:  . Точки этих прямых будут соответствовать средним выигрышам первого игрока при использовании некоторой смешанной стратегии.
. Точки этих прямых будут соответствовать средним выигрышам первого игрока при использовании некоторой смешанной стратегии.
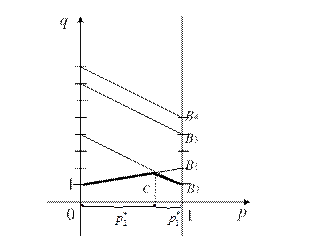
Рис. 6.1
Нижняя ломаная соответствует среднему гарантированному выигрышу. Вершина ломаной - максимальный гарантированный выигрыш. Следовательно, цена игры и оптимальные стратегии определяются 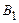 и
и 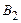 .
.
3) Составим уравнения этих прямых и определим цену игры с и смешанные стратегии:
 и
и 
Ответ: 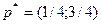 ,
,  , с= 7/4.
, с= 7/4.
Замечание 6.1. При решении игры, заданной матрицей 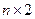 , минимально удаленная от оси q точка верхней ломанной (ограничивающей максимальные средние выигрыши первого игрока) соответствует минимально возможному проигрышу второго игрока для оптимальных смешанных стратегий обоих игроков.
, минимально удаленная от оси q точка верхней ломанной (ограничивающей максимальные средние выигрыши первого игрока) соответствует минимально возможному проигрышу второго игрока для оптимальных смешанных стратегий обоих игроков.
3) Вышеуказанные способы решения задач ТИ имеют ограничение на использование. Способ сведения задачи ТИ к ЗЛП по теореме 6.5 лишен этого недостатка.
Задача. Предприятие может выпускать два вида продукции  , получая при этом прибыль, зависящую от спроса, который может быть в одном из четырех состояний
, получая при этом прибыль, зависящую от спроса, который может быть в одном из четырех состояний 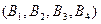 . Дана матрица
. Дана матрица 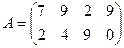 , элементы которой характеризуют прибыль, которую получит предприятие при выпуске i -й продукции при j- м состоянии спроса. Определить оптимальные пропорции в выпускаемой продукции с помощью линейного программирования, гарантирующие среднюю величину прибыли при любом состоянии спроса, считая его неопределенным.
, элементы которой характеризуют прибыль, которую получит предприятие при выпуске i -й продукции при j- м состоянии спроса. Определить оптимальные пропорции в выпускаемой продукции с помощью линейного программирования, гарантирующие среднюю величину прибыли при любом состоянии спроса, считая его неопределенным.
Решение задачи:
Упростим платежную матрицу, отбросив стратегии заведомо невыгодные или дублирующие. Так, вторая стратегия (второй столбец) является явно невыгодной по сравнению с первой (элементы второго столбца больше элементов первого столбца), так как цель игрока В – уменьшить выигрыш игрока А. Поэтому второй столбец можно отбросить. Получим матрицу 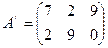 .
.
Замечание 6.2. Если в платежной матрице элементы k -той строки не меньше соответствующих элементов s -той, s -тая строка вычеркивается.
Замечание 6.3. Если элементы l -того столбца не превосходят соответствующих элементов r -того столбца, то r -тый столбец вычеркивается.
Найдем нижнюю и верхнюю цену игры:
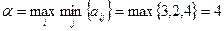 ,
,
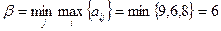 .
.
Следовательно,  .
.
Согласно теореме 6.5 о цене игры 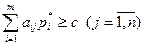 и
и 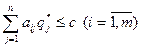 . Пусть для определенности с>0. Разделим каждое неравенство на с:
. Пусть для определенности с>0. Разделим каждое неравенство на с:
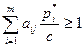 и
и 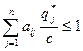 .
.
Обозначив 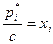 (6.1) и
(6.1) и 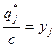 (6.2) и приняв во внимание, что первый игрок стремится по возможности увеличить цену игры, тогда как второй – уменьшить ее величину, и так как
(6.2) и приняв во внимание, что первый игрок стремится по возможности увеличить цену игры, тогда как второй – уменьшить ее величину, и так как 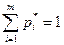 и
и 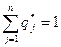 , то
, то
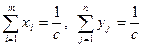 .
.
В результате получим пару взаимно двойственных задач:
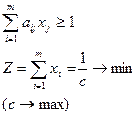 и
и 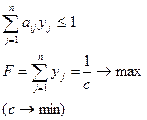 .
.
Решив одну из этих задач, получим решение другой. Решать удобнее ту задачу, в которой число столбцов больше числа строк. При этом необходимо выполнить обратный переход:
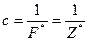 ,
, 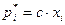 ,
, 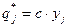 . (6.3)
. (6.3)
Вернемся к решению поставленной задачи. По матрице игры 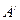 составим пару двойственных задач линейного программирования:
составим пару двойственных задач линейного программирования:
 и
и 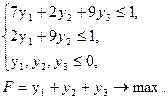
Решим вторую задачу основным симплекс-методом, предварительно преобразовав математическую модель задачи к канонической форме с предпочтительными переменными:
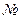
| 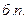
| 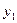
| 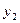
| 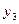
| 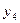
| 
| 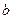
|
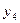 * *
| |||||||

| |||||||
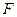
| -1* | -1 | -1 | ||||
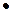 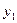
| 2/7 | 9/7 | 1/7 | 1/7 | |||
 * *
| 59/7 | -18/7 | -2/7 | 5/7 | |||
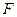
| -5/7* | 2/7 | 1/7 | -1/7 | |||
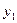
| 49/413 | ||||||
 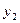
| -18/59 | -2/59 | 7/59 | 5/59 | |||
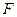
| 28/413 | 49/413 | 5/59 | -84/413 |
Получили оптимальный план решения второй задачи: 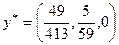 ,
, 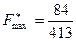 . Тогда, используя соответствие между переменными исходной и двойственной задач, выпишем оптимальное решение первой задачи:
. Тогда, используя соответствие между переменными исходной и двойственной задач, выпишем оптимальное решение первой задачи:  ,
,  .
.
По формуле 6.3 получим цену игры  .
.
Используя формулы 6.1 и 6.2, получим оптимальные смешанные стратегии игроков:
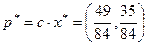 и
и 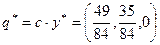 .
.
Ответ: 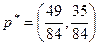 ,
,  ,
,  .
.
Таким образом, в ответе указаны оптимальные пропорции в выпускаемой продукции, гарантирующие среднюю величину прибыли  при любом состоянии спроса.
при любом состоянии спроса.
Педагогический комментарий. Данное лекционное занятие закладывает основы для формирования следующих профессиональных умений студентов-экономистов: умение выявлять проблемы экономического характера при анализе конкретных ситуаций, предлагать способы их решения и оценивать ожидаемые результаты; умение разрабатывать и обосновывать варианты эффективных производственно-технологических решений; умение ставить цель и формулировать задачи, связанные с профессиональной деятельностью, умение использовать для их решения методы изученных дисциплин; умение логически мыслить; умение совершенствовать составление оперативно-производственного плана с использованием инструментария математического программирования; умение эффективно управлять экономическими процессами и регулировать использование комплекса имеющихся ресурсов; умение вырабатывать компромиссные рекомендации при конфликтных ситуациях принятия решения.
Тема 6. Матричные статистические игры
План лекции:
1. Понятие статистической игры
2. Критерии выбора оптимальной стратегии при решении
статистической игры
3. Кооперативные игры
|
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 1161; Нарушение авторских прав?; Мы поможем в написании вашей работы!