Решение ТЗ методом потенциалов

Сущность метода: сначала находят опорный план решения задачи, а затем последовательно улучшают его до тех пор, пока не будет получен оптимальный план. Существует несколько способов построения опорного плана.

Определение 8.1. Опорный план называется невырожденным, если количество заполненных клеток равно n + m – 1.

Задача. Решить ТЗ, заданную следующей таблицей:

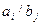
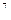
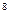
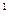
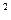
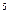
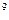
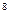
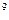
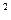
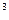
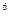
Так как 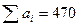и 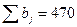, то модель ТЗ закрытая.

1) Метод северо-западного угла.

Метод позволяет за n+m– 1 шаг заполнить клетки таблицы таким образом, чтобы удовлетворить все потребности, исчерпав при этом все запасы. Заполнение клеток таблицы начинается с левой верхней клетки для 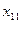и заканчивается клеткой .

Получим опорное решение по методу северо-западного угла, заполнив таблицу:

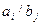
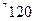
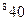
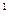
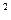
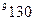
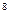
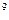
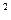
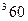
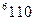
Получен невырожденный план, так как число заполненных клеток равно 6, что совпадает со значением выражения n+m –1=4+3–1=6.

Определим значение целевой функции для данного плана решения задачи .

2) Метод минимального элемента.

Последовательно заполняются клетки с наименьшей стоимостью перевозок. Если имеется несколько клеток с наименьшей стоимостью, то из них выбирается любая. Клетка заполняется максимально возможным числом, при этом исчерпываются либо запасы, либо потребности.

Найдем опорное решение по методу минимального элемента, заполнив таблицу:

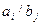
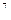
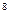
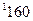
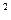
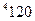
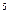
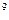
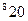
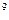
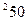
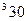
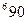
Получен невырожденный план.

Значение целевой функции для данного плана решения задачи .

3) Метод аппроксимации Фогеля.

В таблице по строкам и столбцам определяется разность между двумя наименьшими тарифами. Наибольшая разность помечается кружком О. Далее в строке (столбце) с наибольшей разностью заполняется клетка с наименьшим тарифом. Строки (столбцы) с нулевым остатком груза в дальнейший расчет не принимаются. На каждом этапе заполняется только одна клетка.

Найдем опорное решение по методу аппроксимации Фогеля, заполнив таблицу:

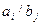
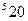
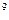
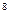
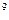
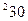
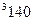
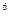
Получен невырожденный план.

Значение целевой функции для данного плана решения задачи .

Как правило, при построении опорного плана вышеуказанными методами выполняется соотношение .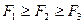

Замечание 8.1. При нахождении начального опорного плана перевозок возможен случай вырождения, когда в результате вычислений значения поставки получается, что потребности в пункте удовлетворены, а запасы в пункте исчерпаны. Тогда одновременно из рассмотрения выбывают строка и столбец. В этом случае рекомендуется осуществить в одну из клеток выбывающих строки и столбца (в клетку с наименьшей стоимостью) так называемую нулевую поставку. Клетка с такой поставкой считается заполненной.

Дата добавления: 2014-01-13