Комплексные частотные характеристики

Всякую комплексную величину H (j ω) можно представить в показательной, тригонометрической и алгебраической форме (3.6):

;

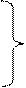
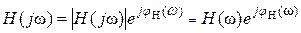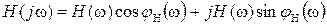; (3.6)

.

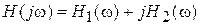Величина H( ω) = │H (j ω) │ является модулем передаточной функции.

Зависимость модуля комплексной передаточной функции от частоты называется амплитудно-частотной характеристикой цепи (АЧХ) КПФ (рис. 3.2, а).

Величина φ_H(ω) = arg H (j ω) – аргумент комплексной передаточной функции. Зависимость φ(ω) от частоты называют фазо-частотной характеристикой цепи (ФЧХ) КПФ (рис. 3.2, б).

Величины

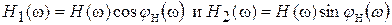(3.7)

есть вещественная и мнимая части комплексной передаточной функции.

Из (3.6) и (3.7) можно получить выражения модуля (АЧХ) и аргумента (ФЧХ) комплексной передаточной функции

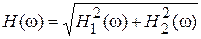; (3.8)

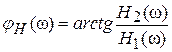. (3.9)

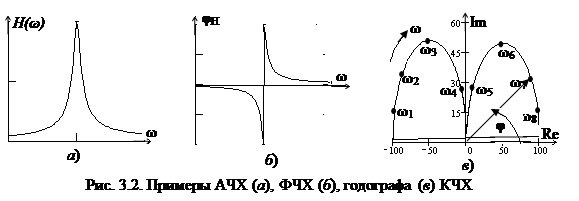АЧХ и ФЧХ цепи можно изобразить единым графиком, если построить зависимость КПФ H (j ω) от частоты ω на комплексной плоскости. При этом конец вектора H (j ω опишет некоторую кривую, которая называется годографом комплексной передаточной функции (рис. 3.2, в). На годографе указывают точки, соответствующие некоторым значениям частоты ω, и стрелкой показывают направление перемещения конца вектора при увеличении частоты.

Совокупность АЧХ, ФЧХ и годограф составляет комплексные частотные характеристики (КЧХ). КЧХ являются наиболее фундаментальными понятиями теории цепей и широко используются на практике.

В ряде случаев частотные характеристики цепи могут изменяться в очень широких пределах, поэтому более удобно их оценивать в логарифмическом масштабе. С этой целью для оценки АЧХ вводят понятие логарифмической амплитудно-частотной характеристики (ЛАХ):

K = 20lg H (ω).

Оценивается ЛАХ в децибелах (дБ). В активных цепях K называют еще логарифмическим усилением. Для пассивных цепей вместо коэффициента усиления оперируют ослаблением цепи

A = 20lg[1/ H (ω)],

которое также оценивается в децибелах.

Дата добавления: 2014-01-13