Линия без потерь

Вторичные параметры и уравнения передачи. Реальная линия всегда обладает потерями. Однако в ряде случаев удобно считать линию идеальной, т. е. не имеющей потерь: R ₁ = G ₁ = 0. Такая идеализация оправдана для коротких по длине линий, работающих на сверхвысоких частотах (фидеров, элементов радиотехнических устройств, полосковых линий и др.), где выполняются условия R ₁ << ω L и G ₁ << ω C.

Коэффициент распространения линии без потерь

Отсюда коэффициент ослабления α = 0, а коэффициент фазы 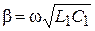линейно зависит от частоты.

Коэффициент фазы β связан с длиной волны электромагнитного колебания. Длиной волны λ называется расстояние между двумя точками, взятыми в направлении распространения волны, фазы в которых отличаются на 2π. Следовательно, βλ = 2π иλ = 2π / β.

Волновое сопротивление линии без потерь

является чисто резистивным (активным).

Уравнения передачи линии без потерь получаются из (6.29), если учесть, что ch γ l = ch j β l = cos β l и sh γ l = sh j β l = j sin β l:

(6.33)

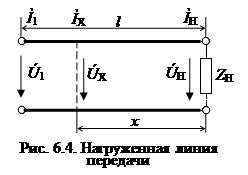При анализе процессов в линии без потерь общепринято расположение той или иной точки на линии характеризовать ее удаление не от начала линии, как это делали прежде, а от конца линии (от нагрузки) (рис. 6.4). В этом случае уравнения передачи линии без потерь, выражающие комплексные значения напряжения и тока в произвольной точке линии x, отсчитанной от ее конца, записываются в виде:

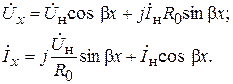(6.34)

Формула (6.30) входного сопротивления для линии без потерь примет следующий вид

. (6.35)

Дата добавления: 2014-01-13