Пример 11. Определим медиану заработной платы рабочих

Пример 10.

Определим медиану заработной платы рабочих.

Таблица 5.7.

Месячная з/п, руб.	Число рабочих	Сумма накопительных частот
		8 (2+6)
		24 (8+16)
		—
		—

Для определения медианы надо подсчитать сумму накопленных частот ряда. Наращивание итога продолжается до получения накопленной суммы частот, превышающей половину. В нашем примере сумма частот составила ее половина - 20.

Накопленная сумма частот ряда получилась равной Варианта, соответствующая этой сумме, т.е. 160 руб., и есть медиана ряда.

Если же сумма накопленных частот против одной из вариант равна точно половине сумме частот, то медиана определяется как средняя арифметическая этой варианты и последующей.

Таблица 5.8.

Месячная з/п, руб.	Число рабочих	Сумма накопительных частот
		8 (2+6)
		20 (8+12)
		—
		—

Медиана будет равна:

Ме = (150 + 170) / 2 = 160 руб.

Рассмотрим расчет медианы в интервальном вариационном ряду.

Медиана интервального вариационного ряда распределения определяется по формуле

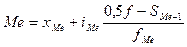
где 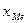— начальное значение интервала, содержащего медиану;

— величина медианного интервала;

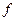— сумма частот ряда;

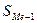— сумма накопленных частот, предшествующих медианному интервалу;

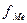— частота медианного интервала.

Пример 12.

Таблица 5.9.

Группы предприятий по числу рабочих	Число предприятий	Сумма накопительных частот
100 — 200
200 — 300		4 (1+3)
300 — 400		11 (4+7)
400 — 500		41 (11+30)
500 — 600		—
600 — 700		—
700 — 800		—
ИТОГО

Определим прежде всего медианный интервал. В данной задаче сумма накопленных частот, превышающая половину всех значений (41), соответствует интервалу 400 - 500. Это и есть медианный интервал, в котором находится медиана. Определим ее значение по приведенной выше формуле.

Известно, что:

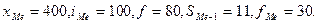
Следовательно,

.

1. Мода (Mo) – величина признака, наиболее часто встречающаяся в совокупности, т.е. имеющая наибольшую численность в ряду распределения.

а) В дискретном ряду распределения мода определяется визуально.

б) В интервальном ряду распределения визуально можно определить только интервал, в котором заключена мода, который называется модальным интервалом. Мода будет равна:

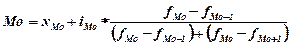
где х_Мо – нижняя граница модального интервала;

i_Мо – величина модального интервала;

f_Мо – частота модального интервала;

f_Мо-1 – частота, предшествующая модальному интервалу;

f_Мо+1 – частота интервала, следующего за модальным.

2. Медиана (Me) – значение признака, приходящееся на середину ранжированного ряда, т.е. делящее ряд распределения на две равные части.

а) В дискретном ряду распределения определяется номер медианы по формуле:

Номер медианы показывает то значение показателя, которое и является медианой.

б) В интервальном ряду распределения медиана рассчитывается по следующей формуле:

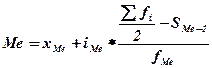
где х_Ме – нижняя граница медианного интервала;

i_Ме – величина медианного интервала;

f_Ме – частота медианного интервала;

S _Ме-1 – сумма накопленных частот, предшествующих медианному интервалу;

åf_i/2 – полусумма частот ряда.

Мода и медиана могут быть определены графически.

Дата добавления: 2014-01-13