Уравнение плоской волны

Волновой поверхностью (фронтом волны) называется геометрическое место точек, колеблющихся все время одинаково, т.е. в одной и той же фазе. Если волновыми поверхностями являются плоскости, перпендикулярные направлению распространению волны, то такие волны называются плоскими.

Пусть волна распространяется вдоль оси ох без затухания так, что амплитуда колебаний всех точек одинакова и равна А. Зададим колебание точки с координатой х=0 (источник колебаний) уравнением:

.

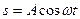До точки с некоторой произвольной координатой х возмущение от начала координат дойдет через время 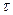, поэтому колебания этой точки запаздывают (рис. 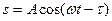1.):

(1)

где , то (1) можно переписать

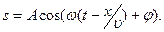(2)

Рис.1.

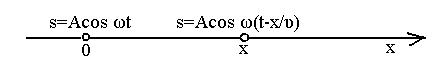
Это и есть уравнение плоской синусоидальной волны, распространяющейся вдоль оси абсцисс («-» при движении волны в положительном направлении оси х, «+» в отрицательном). Аргумент при косинусе называется фазой волны. Скорость распространения фиксированной фазы колебаний называют фазовой. Предположим, что =const. Продифференцировав это равенство, получаем 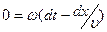, откуда

.

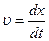Следовательно, скорость распространения фиксированной фазы колебаний и есть скорость распространения волны.

Кроме фазовой скорости различают еще групповую скорость, которую вводят тогда, когда реальная волна не может быть представлена одним гармоническим уравнением (2), а является суммой группы синусоидальных волн.

Длиной волны называют расстояние между двумя точками, фазы которых в один и тот же момент времени отличаются на 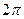. Она равна расстоянию, пройденному волной за период колебания:

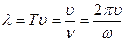. (3)

Величина

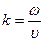
называется волновым числом. Сравнив с (3) получим

.

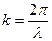Волновое число показывает, сколько длин волн укладывается на расстоянии, равном 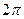метров.

Таким образом, можно (2) переписать в виде:

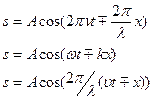(4).

Уравнение волны (4) – одно из возможных решений общего дифференциального уравнения с частными производными, описывающего процесс распространения возмущения в среде. Такое уравнение называют волновым.

Продифференцируем (2) дважды по времени и по координате:

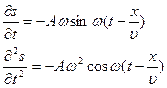
. (5)

Сравнивая вторые производные в (5) (cos), получаем одномерное волновое уравнение

.

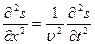Дата добавления: 2014-01-11