Расчет сводного индекса

Рассмотрим методику расчета сводных индексов на конкретном примере.

Имеются следующие данные о реализации овощной продукции на городском рынке:

Цены разных товаров, реализуемых в розничной торговле, складывать неправомерно, однако с экономической точки зрения допустимо суммировать их товарооборот. Если сравнивать товарооборот в текущем периоде с его величиной в базисном периоде, то получим сводный индекс товарооборота:

Рассчитаем индекс товарооборота для примера 1:

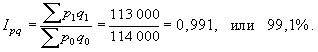
Мы получим, что товарооборот в целом по рассматриваемой товарной группе в текущем периоде по сравнению с базисным уменьшился на 0,9% (100-99,1).

На величину данного индекса оказывает влияние как изменение цен на товары, так и изменение объемов их реализации. Для того чтобы оценить изменение только цен (индексируемой величины), необходимо количество проданных товаров (веса индекса) зафиксировать на каком-либо постоянном уровне. При исследовании динамики таких качественных показателей, как цена, себестоимость, производительность труда, количественный показатель обычно фиксируют на уровне текущего уровня. Таким способом получают сводный индекс цен:

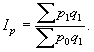
Числитель данного индекса содержит фактический товарооборот текущего периода. Знаменатель же представляет собой условную величину, показывающую, каким был бы товарооборот в текущем периоде при условии сохранения цен на базисном уровне. Поэтому соотношение этих двух категорий и отражает изменение цен. Изменение же количества реализованной продукции не влияет на величину индекса.

Вычислим сводный индекс цен для примера 1:

Следовательно, по данной товарной группе цены в октябре по сравнению с августом снизились на 31,7%.

Числитель и знаменатель сводного индекса цен можно интерпретировать с точки зрения потребителей. Числитель представляет собой сумму денег, фактически уплаченных покупателями за приобретенные в текущем периоде товары. Знаменатель же показывает, какую сумму покупатели заплатили бы за те же товары, если бы цены не изменились. Разность числителя и знаменателя будет отражать величину экономии (если знак «-») или перерасхода (если знак «+») покупателей от изменения цен:

Третьим индексом в данной индексной системе является сводный индекс физического объема реализации. Он характеризует изменение количества проданных товаров не в денежных, а в физических единицах измерения:

Весами в данном индексе выступают цены, которые фиксируются на базисном уровне.

Индекс физического объема реализации в примере 1 составит:

Физический объем реализации в октябре по сравнению с августом увеличился в 1,45 раза, или на 51 500 руб. (165 500 - 114 000).

Между рассчитанными индексами существует следующая взаимосвязь:

Ip × Iq = Ipq.

Используя взаимосвязь индексов, проверим правильность вычислений в примере 1:

I_pq = I_p × I_q = 0,683 × 1,452 = 0,991, или 99,1%.

Следовательно, снижение товарооборота (на 0,9%) обусловлено ростом объема проданной продукции (на 45,2%) и снижением цен (на 68,3%), что в абсолютном выражении составило -1000 руб. (-52 500 + 51 500).

Мы рассмотрели применение агрегатных индексов в анализе товарооборота цен и физического объема реализации. При анализе результатов производственной деятельности промышленного предприятия, приведенные сводные индексы соответственно называются индексом стоимости продукции, индексом оптовых цен и индексом физического объема продукции.

Контрольные вопросы

1.Что в статистике называют индексом?

2. Какие задачи решают при помощи индексов?

3. Что характеризуют индивидуальные индексы? Приведите примеры.

4. В чем сущность общих индексов?

5. Для чего необходимо деление на индексы объемных (количественных) и качественных показателей и какая система взвешивания принята в теории индексов?

6. Как исчисляется агрегатный индекс стоимости продукции (товарооборота в фактических ценах) и что он характеризует?

7. Как исчисляется агрегатный индекс физического объема продукции (товарооборота) и что он характеризует? Напишите формулу.

8. Когда возникает необходимость преобразования индекса физического объема в средней арифметический и средний гармонический? Каким образом происходят такие преобразования? Покажите на примерах.

9.Как исчисляют агрегатные индексы цен (Паше и Ласпейреса). себестоимости, производительности труда и что они показывают? Напишите их формулы.

10. Когда возникает необходимость преобразования агрегатного индекса цен в средний гармонический и средний арифметический? Каким образом происходят такие преобразования? Покажите на примере.

11. Какой вариант агрегатных индексов качественных показателей используют при расчете индекса потребительских цен и почему?

12. Что называется индексом переменного состава, как он исчисляется и что характеризует? Напишите его формулу.

13. Какой индекс называется индексом постоянного состава, как он исчисляется и что характеризует?

14. Что характеризует индекс структурных сдвигов и как он исчисляется?

15. Какая взаимосвязь существует между индексами переменного, постоянного состава и структурных сдвигов?

16. Как строятся базисные и цепные индексы и какая между ними существует взаимосвязь?

17. Что представляют собой индексы с постоянными и переменными весами?

18. Что представляет собой система взаимосвязанных индексов. Для чего она применяется?

19. В чем выражается взаимосвязь индексов цен, физического объема и товарооборота? Как практически она используется?

20. Какая система взаимосвязанных индексов используется при анализе себестоимости, физического объема и затрат в производстве?

21. Как определить долю влияния различных факторов на изменение результативного?

Дата добавления: 2014-01-13