Види виробничих функцій

Існують двофакторні та багатофакторні виробничі функції

У наведеному нижче списку функцій вони розташовуються в порядку зростаючої складності їх у запису й, відповідно, збільшення кількості необхідних для цього параметрів. Усі ці функції допускають можливість їх модифікації:

1. Функція з фіксованими пропорціями чинників (функція Леон­тьєва).

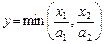, (5.1)

де а ₁, а ₂ — параметри.

Функція Леонтьєва призначена в основному для моделювання строго детермінованих технологій, які не допускають відхилення від технологічних норм і нормативів щодо використання ресурсів на одиницю продукції. Як правило, вона використовується для формалізованого опису дрібномасштабних або цілком автоматизованих об’єктів.

2. Функція Кобба—Дугласа

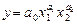. (5.2)

Тут також використовується кілька систем гіпотез, що виокремлюють клас функцій Кобба—Дугласа серед двічі диференційованих функцій від двох змінних:

а) еластичності випуску за чинниками є постійними:

.

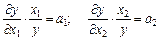Розв’язок цієї системи диференційних рівнянь у частинних похідних першого порядку належить до класу функцій Кобба—Дугласа;

б) еластичність функції за одним із чинників є постійною, і функція є однорідною;

в) функція є однорідною, а еластичності зменшення чинників за Алленом та Михайловським дорівнюють одиниці;

г) гранична продуктивність кожного чинника є пропорційною його середній продуктивності;

д) функція є однорідною як функція від х ₁, х ₂ і як функція від х ₁ за будь-якого фіксованого х ₂;

є) функція може бути отримана з функції з постійною еластичністю шляхом здійснення заміни виду

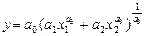
та граничного переходу а ₃ ® 0. Функція Кобба—Дугласа найчастіше використовується для формалізованого опису середньомасштабних господарських об’єктів та економіки країни.

3. Лінійна функція

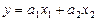. (5.3)

Передумови та гіпотези:

а) граничні продуктивності чинників є постійними:

,

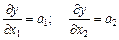а в нулі функція набуває нульового значення;

б) гранична продуктивність одного з чинників є постійною, і функція однорідна першого степеня:

;

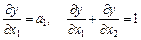в) функція однорідна, й еластичність заміни чинників, за Алленом, є нескінченною;

г) еластичність випуску за чинниками обернено пропорційна їхній середній продуктивності.

Лінійна функція застосовується для моделювання великомасштабних систем (велика галузь, народне господарство в цілому), у яких випуск продукції є результатом одночасного функціонування великої кількості різноманітних технологій.

Функція Аллена:

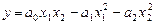(5.4)

визначається за такими умовами: швидкості зростання граничних продуктивностей є постійними, і функція є однорідною.

Функція Аллена за a ₁, a ₂ > 0 призначається для формалізованого опису виробничих процесів, у яких надмірне зростання будь-якого з чинників негативно впливає на обсяг випуску продукції. Зазвичай така функція використовується для формалізованого опису дрібномасштабних виробничих систем з обмеженими можливостями переробки ресурсів.

4. Функція постійної еластичності заміщення чинників (функція CES):

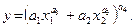(5.5)

Передумови та гіпотези:

Функція є однорідною, й еластичність заміщення чинників є постійною.

Функція CES застосовується у разі відсутності точної інформації щодо рівня взаємозаміни виробничих чинників, і разом з тим є підстави вважати, що цей рівень суттєво не зміниться за зміни обсягів залучених ресурсів, тобто коли економічна технологія має властивість певної стійкості щодо певних пропорцій чинників.

5. Функція Солоу:

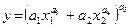(5.6)

характеризується тим, що величина відсоткової зміни граничної норми заміщення чинників, що пов’язане зі зміною одного з чинників на один відсоток, не залежить від початкового рівня чинників.

. Функція Солоу може використовуватись у моделюванні системи різних масштабів.

6. Багаторежимна функція:

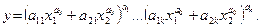(5.7)

Функція є однорідною, еластичність функції за першим аргументом є згладженою k -рівневою спадною ступінчастою функцією.

Багаторежимна функція — одна з найзагальніших. Вона використовується для формалізованого опису та моделювання процесів, у яких рівень віддачі кожної додаткової одиниці ресурсу стрибкоподібно змінюється залежно від співвідношення чинників. Функцію доцільно застосовувати за наявності апріорної інформації щодо кількості режимів k, а інколи й щодо величини «перехідної» області між режимами (чим більше 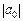, тим чіткіше виокремлюються режими).

Багатофакторні виробничі функції

В економіко-математичному моделюванні широко використовують багатофакторні виробничі функції.

Один із найбільш раціональних способів переходу від двофакторних до багатофакторних функцій полягає в такому.

Розгляньмо двофакторну функцію:

y = j₁ (x ₁, x ₂). (5.8)

Аргумент x ₂ цієї функції розглянемо як узагальнений показник, що залежить також від двох інших чинників x ₃, x ₄:

x ₂ = j₂(x ₃, x ₄),

де j₂ — деяка функція. Підставляючи цей вираз у формулу (5.8), отримаємо трифакторну функцію

y = j₁(x ₁, j₂(x ₃, x ₄)),

що виражає залежність показника 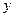від аргументів x ₁, x ₃, x ₄. Цей процес можна продовжити, вважаючи, зокрема, що х ₃, у свою чергу, залежить від деяких чинників.

У загальному вигляді: якщо задано (п – 1) двофакторних функцій j₁(x ₁, x ₂), j₂(x ₃, x ₄), j _{n –1}(x _{2 n –3}, x _{2 n –2}), то дістанемо п-факторну функцію:

y = f (x ₁,..., x_n)

у результаті послідовної підстановки їх. Операція такої підстановки (суперпозиції) має очевидний економічний сенс: другий аргумент, наприклад двофакторної функції, послідовно подається у вигляді залежності від показників нижчих (деталізованих) рівнів.

Для виробничих функцій від n змінних справедливими є твердження, які показують, що клас функцій, поданих у вигляді суперпозиції будь-яких двофакторних функцій, є досить широким. Строго доводиться, зокрема, що будь-яка неперервна функція f (x ₁, …, x_n) від n змінних (за умови n ³ 4) може бути подана у вигляді суперпозиції неперервних функцій від трьох змінних.

Дата добавления: 2014-01-11