Лекция 5,6

ПОКАЗАТЕЛИ УПРУГИХ И ПРОЧНОСТНЫХ СВОЙСТВ ГОРНЫХ ПОРОД.

В общем случае горные породы не соответствуют модели упругого тела. Например, на вид зависимости напряжений от деформации влияет скорость нагружения. Поэтому следует помнить, что определение показателей упругих свойств горных пород не означает, что горные породы — идеально упругие тела, а преследует цель, оценить проявление упругих свойств в более сложной модели тела при стандартных методах испытания.

Для минералов и некоторых горных пород зависимость нагрузки от перемещения при деформировании линейная, т. е. как бы выполняется закон Гука. Модуль упругости в этом случае можно определить по известной формуле. В случае нелинейной зависимости при небольшой кривизне модуль упругости можно с достаточной точностью также определить по известной формуле. Если же кривизна значительна, то график нагрузка — перемещение разбивают на ряд. участков с одинаковым шагом по нагрузке. По участкам значение модуля также определяется по известной формуле, а среднее значение по формуле

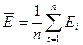б

Ниже приведены значения модуля Юнга (E-10~i, МПа) при одноосном сжатии различных пород.

Глинистые сланцы............1,5—2,5 Песчаники...................3,3 —7,8 Известняки...................1,3—3,5 Мрамор......................3,9—9,2

Доломиты..................2,1 – 16,5 Граниты......................<6,0 Базальты......................<9,7 Кварциты...................7,5 – 10,0

Экспериментально установлено, что проявление упругих свойств горных пород зависит от ряда факторов. Например, между значе­ниями модулей Юнга при растяжении E _Р, изгибе Е _И и сжатии Е сж существует неравенство Е_Р<Е_И<Е_СЖ. Модуль Юнга при изгибе в 1,1—1,3 раза больше, чем при растяжении, и составляет 0,25— 0,35 от модуля Юнга при сжатии.

Если основной породообразующий минерал, входящий в состав породы имеет высокий модуль Юнга, то и порода имеет высокий модуль, но модуль Юнга породы всегда будет меньше модуля Юнга минерала. Это объясняется тем, что модуль Юнга главным образом зависит от сил взаимодействия в кристаллических решетках, которые в горных породах по местам контактов зерен значительно слабее, чем внутри зерен минералов. Поэтому модуль Юнга породы в целом не может превышать максимальный модуль минералов, слагающих данную породу.

Установлено, что при прочих одинаковых условиях повышение песчанистости породы ведет к увеличению ее модуля Юнга. Модуль Юнга у глинистых сланцев возрастает по мере увеличения их карбонатности. Значительно влияют на величину Е состав и строение цементирующего вещества у обломочных горных пород. Так, песчаники с карбонатным цементом обладают большим модулем Юнга, чем те, которые имеют глинистый цемент.

На модуль Юнга влияют также пористость, слоистость и сланцеватость пород: с увеличением пористости он уменьшается; для глинистых сланцев в направлении, перпендикулярном к сланцеватости, модуль Юнга меньше, чем в направлении, параллельном ей.

При прочих одинаковых условиях с увеличением влажности пород Е уменьшается. Например, при увеличении влажности глинистой породы от 3 до 14 % модуль Юнга уменьшается от 716 до 314 МПа, а при увеличении влажности от 14 до 23 % он уменьшается от 314 до 29 МПа.

В горных породах необратимые деформации появляются даже при незначительных нагрузках по сравнению с разрушающими, хотя при этом и не нарушается (в пределах точности опытов) прямая пропорциональность между напряжениями и деформациями. Необратимые деформации в случае многократного деформирования становятся равными нулю, а модуль упругости пород возрастает. Ниже приведены значения коэффициента Пуассона различных пород.

Глины пластичные............. 0,38—0,45

Глины плотные.................0,25-0,35

Глинистые сланцы.............. 0,10-0,20

Известняки................... 0,28—0,33

Каменная соль...................... 0,44

Песчаники......................0,30-0,35

Гранит.........................0,26-0,29

На коэффициент Пуассона влияют те же факторы, что и на модуль Юнга: метод определения (µ₀<µ_сж), структура, текстура и глубина залегания породы. Чем глубже залегает порода, чем плотнее она и старше по возрасту, тем меньше для нее µ.

В практике исследований горных пород модуль деформации при сдвиге G определяют лишь в тех случаях, когда испытывают образцы горных пород на кручение. Модуль G нетрудно вычислить, если известны модуль Юнга и коэффициент Пуассона по известной формуле. Однако из-за нелинейности зависимостей между напряжениями и деформациями для горных пород и большого различия между Е _р и Е _сж такая оценка модуля G будет весьма приближенной.

Существует ряд методов определения динамических упругих характеристик пород. Наибольшее распространение получил метод, основанный на измерении скорости распространения продольных и поперечных волн в горных породах.

На достаточно больших образцах пород, имитирующих полупространство, определяются скорости распространения продольных с и поперечных с _п упругих волн. Это позволяет вычислить динамический коэффициент Пуассона µ_Д и модуль упругости Е _Д:

.

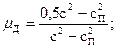
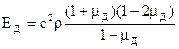По скорости распространения поперечной волны с _П непосредственно можно определить динамический модуль деформации при сдвиге G _Д:

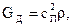
В табл. приведены модули Юнга Е, определенные в статических условиях, и рассчитанные по скорости прохождения про­дольных и поперечных волн.

Таблица Статические и динамические упругие характеристики горных пород (по данным Н.М. Филимонова)

Горная порода	Е •10^-2, МПа	µД	Е д-10^-2, МПа	Е Д / Е
Ангидрит Известняк   Доломит		0,27 0,34 0,36 0,26 0,31		3,66 3,52 2,88 4,95 3,04

Из таблицы видно, что динамический модуль Юнга больше статического в несколько раз. Это еще раз подтверждает, что мате­матическая модель горной породы значительно сложней упругой модели. В случае использования упругой модели для решения практических задач необходимо, чтобы упругие характеристики пород определялись в тех условиях, для которых решается та или иная задача.

О порядке величин прочности горных пород при одноосном сжатии s_сж (в МПа) можно судить по приведенным ниже данным УфНИИ.

Известняки пелитоморфные...................... 80—130

Известняки мелкокристаллические............... 100—170

Известняки органогенно-обломочные............. 130—200

Известняки окремнелые.........................200—260

Доломиты мелкокристаллические................... 245

Алевролиты................................... 40—120

Песчаники...................................... 28—80

Мергели алевритистые.......................... 130—170

Ангидриты....................................150—190*

* Ангидриты, по-видимому, частично доломитнзированы.

Из приведенных данных видно, что s_сж для одноименных пород колеблется в широких пределах. Вместе с тем прочность пород разного минералогического состава иногда одна и та же. Эти данные показывают, что на прочность горных пород влияют не только их минералогический состав, но и ряд других факторов, в частности, структура и текстура породы, глубина залегания и т. п.

Сравнение прочности горных пород при простых видах испытаний удобно провести в относительных величинах. Результаты расчетов для некоторых горных пород приведены в таблице.

Таблица Относительная прочность горных пород (в %)

Горная порода	Сжатие	Сдвиг	Изгиб	Растяжение
Глинистые сланцы Песчаники Гипсы Известняки		— 10—12 15 —	6—20 8—10	2-5 4—10

Рассматривая прочность горных пород в зависимости от вида испытания, нетрудно заметить, что наибольшее сопротивление горные породы оказывают в случае сжатия, а при других видах испытаний их прочность ниже, т. е. имеет место неравенство s_сж > t_c > >s_и > s_р.

С точки зрения разрушения горных пород наивыгоднейшим видом деформирования является растяжение, поэтому во время конструирования породоразрушающих инструментов следует учитывать этот фактор.

Натурные испытания горных пород в скважинах осуществить очень сложно. Поэтому большое значение имеет изучение деформирования и разрушения горных пород в условиях, моделирующих их естественное залегание, вскрытие их скважиной и воздействие на них породоразрушающих инструментов.

ОСНОВНЫЕ СХЕМЫ ИСПЫТАНИЙ ГОРНЫХ ПОРОД В УСЛОВИЯХ ВСЕСТОРОННЕГО СЖАТИЯ. ПОВЕДЕНИЕ ГОРНЫХ ПОРОД.

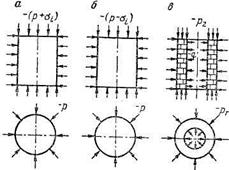Основные схемы лабораторного изучения деформирования и разрушения горных пород в условиях всестороннего сжатия приведены на рисунке. По схеме Кармана (рис.) испытываются цилиндрические образцы, предварительно нагруженные всесторонним равномерным давлением р и нагретые до требуемой температуры Т. В процессе испытания увеличивается нагрузка на торцовые поверхности образца при Т = const. Нагружение и всестороннее давление обусловливают следующие компоненты нормальных напряжений в образце:

s_Z = s₃ = - (P + s _i);

s _r = s₁ = s₂ = - P.

Если р = 0 (атмосферное давление), то схема Кармана переходит в схему испытания при одноосном сжатии. Таким образом, испытание на одно­осное сжатие можно рассматривать как частный случай испытания в условиях всесто­роннего сжатия.

По схеме Бокера (рис.) испытываются на растяжение (выдавливание) под действием бокового давления со стороны цилиндрической поверхности предварительно нагруженные, как и по схеме Кармана, цилиндрические образцы. В процессе испытания снижается нагрузка на торцовые поверхности при Т = const. При этом в образце действуют следующие нормальные напряжения:

s_Z = s₃ = - (P - s _i);

s _r = s₂ = s₃ = - P.

В процессе испытаний записывают графики зависимости интенсивности касательных напряжений s _i от деформации e образца. Обработка результатов испытаний аналогична обработке при одноосном сжатии и позволяет получить упругие, пластические и прочностные показатели свойств горных пород.

Использование переменной составляющей напряжений s _i в качестве основного показателя испытаний в условиях всестороннего сжатия обусловлено тем, что она совпадает с интенсивностью касательных напряжений. Подставив значения этих же компонент напряжений в известную формулу, получим среднее напряжение при испытании по первой схеме:

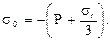
Аналогично получим с₀ для второй схемы испытаний:

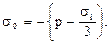
По третьей схеме (см. рис.) испытываются полые цилиндры. Эта схема позволяет получить s1 Ks2 K s3 и резко неоднородное напряженное состояние по толщине стенки полого образца.

Лабораторные установки, реализующие указанные схемы, и ме­тодика работы на них описаны в.

Условие, когда все три главные сжимающие напряжения равны, т.е s₁ = s₂ = s₃, называется равномерным всесторонним сжатием. В этом случае касательные напряжения равны нулю. Из третьей и четвертой теорий прочности следует, что как бы велико ни было среднее давление (s₁ = s₂ = s₃ = s₀), в горных породах не должно возникать ни остаточных деформаций, ни разрушений. Горная порода должна деформироваться только упруго в соответствии с законом Гука.

Эти выводы хорошо подтверждаются при испытаниях плотных однородных горных пород. В процессе деформирования пористых горных пород наблюдаются не только остаточные деформации, но и их разрушение, так как напряженное состояние скелета породы существенно отличается от равномерного всестороннего сжатия.

Испытания при равномерном всестороннем сжатии проводятся для изучения сжимаемости горных пород и минералов. Она характеризуется коэффициентом сжимаемости и модулем объемной деформации при сжатии.

Под коэффициентом сжимаемости b понимают относительное уменьшение объема V c увеличением давления на 1 МПа, т.е.

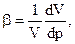
где V о — первоначальный объем при нормальных давлении и температуре.

Если в процессе деформирования соблюдается закон Гука, то

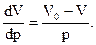
Получим

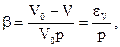
а так как р = s₀, то b = 1/ K, где K модуль деформации.

Таблица. Коэффициенты сжимаемости b некоторых минералов и горных пород по данным Адамса

Минерал, порода	b• 10^5, 1/МПа
p = 196 МПа	р = 981 МПа
Алмаз	0,18	0,1»
Кальцит	1,42	1,42
Полевые шпаты	1,54-1,86	1,36-1,71
Кварц	2,86	2,35
Каменная соль	4,09	3,60
Гранит	2,16	1,92

Из таблицы видно, что по мере увеличения давления коэффициент сжимаемости для таких минералов, как алмаз и кальцит (при давлениях 196 и 981 МПа), не изменяется, а для таких минералов, как полевые шпаты, кварц и каменная соль, он уменьшается. Коэффициент сжимаемости горных пород с увеличением давления, как правило, уменьшается в большей степени, чем коэффициент сжимаемости слагающих их минералов. Это в значительной степени обусловлено уплотнением пород, так как их пористость не равна нулю. Для минералов уменьшение коэффициента сжимаемости с ростом давления не может быть объяснено уплотнением (хотя структура может уплотняться вследствие залечивания дефектов). В этом случае главную роль играет закономерность роста сил отталкивания при сближении частиц.

Коэффициент сжимаемости у горных пород всегда больше и лишь в отдельных случаях равен среднему коэффициенту объемного сжатия минералов, входящих в состав данной породы. Это объясняется менее плотным сложением горной породы, наличием большого количества дефектов на внутренних поверхностях (поверхностях зерен).

Неравномерное всестороннее сжатие может быть в том случае, если хотя бы одно главное напряжение не равно двум другим. В общем случае имеет место условие s ₁ K s ₂ K s ₃.

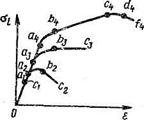
Результаты испытаний по приведенным выше схемам имеют вид зависимостей s ₁ от e при определенных зна­чениях начального давления р. Обобщенный вид зависимостей s ₁ от e приведен на рис.. Индексы соответствуют разным значе­ниям р, причем | p ₁| < | р ₂|< | р ₃| < | p ₄|. На отрезках Оа₁ Оа₂, Оа₃ и Оа₄ соблюдается закон Гука. На отрезках кривой a ₂ b ₂, a ₃ b ₃, a ₄ b ₄ имеет место переходный процесс, заканчивающийся или установившимся пластическим деформированием (отрезки b ₂ c ₂, b ₃ c ₃, b ₄ c ₄), или хрупким разрушением (отрезок a ₁ c ₁). Если пластические сдви­ги локализуются в определенных зонах образца, то развитие де­формирования сопровождается уменьшением s _i; и заканчивается разрушением образца. В этом случае модуль пластичности или отрицателен, или равен нулю.

Если пластические сдвиги равномерно распределены по образ­цу, то наблюдается упрочнение, т. е. развитие деформирования идет лишь при увеличивающемся напряжении (отрезок b ₄ c ₄). Однако и этот процесс заканчивается второй переходной зоной c ₄ d ₄ и далее локализацией деформации и разрушением.

Напряжение, соответствующее точкам а ₁, а ₂, а ₃ и а ₄ обозначает­ся s _is и соответствует пределу текучести породы. Напряжение, отвечающее условию ds _i /de = 0, соответствует прочности породы и обозначается s _ic.

Из рис. видно, что с увеличением всестороннего сжатия увеличиваются как предел текучести, так и прочность породы. Кроме того, наблюдается и изменение процесса пластического деформирования (от хрупкого разрушения до деформирования с упрочнением). В таблице приведены пределы текучести s _is и прочности s _iс образцов горных пород, полученные при испытании по схеме Кармана.

Таблица. Прочностные характеристики горных пород

Параметры	Каменная соль	Мрамор	Доломит	Песчаник
р, МПа	0*
s is, МПа	—		—			—	—	—	—
s iс, МПа		11О

* Одноосное сжатие, принимаем s _is = s _iс

Из табл. видно, что предел текучести каменной соли с увеличением среднего давления изменяется мало, тогда как предел прочности увеличивается более чем в 4 раза. Более существенно увеличение s _is и s _iс у мрамора. Доломит и песчаник при заданных начальных давлениях пластичных свойств не проявляют, однако предел прочности увеличивается в 3—4 раза. Пластическая деформация зависит от всестороннего сжатия, вида породы и ее строения. По данным Б. В. Байдюка, у некоторых разновидностей известняков пластическая деформация достигает 0,07 при давлении 49 МПа и 0,3 при давлении 98 МПа, у ангидритов — от 0,05 до 0,3 при давлениях 98—147 МПа, а у алевролитов — от 0,05 до 0,25 при давлениях 49—196 МПа.

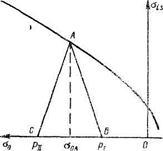
Важнейшим результатом испытаний горных пород при неравномерном всестороннем сжатии является построение зависимости s _is от s ₀, называемой паспортом прочности горных пород или предельной кривой. Для этого при заданных р по известным формулам рассчитывают среднее напряжение, соответствующее полученному значению s _is. Общий вид паспорта прочности горной породы приведен на рис..

Существующие методики испытания при всестороннем сжатии не обеспечивают условия s ₀ = const. При испытании по первой схеме всестороннее сжатие увеличивается, а при испытании по второй схеме — уменьшается.

В первом случае нагружение идет по линии ВА, а s ₀ меняется от p _i до s_0А (рис.).

- т з_п и

- напряжений

- ме Капмана

- (СА)

'

	Рис. Обобщенная зависимость s is от e при различных значениях начального всестороннего сжатия
		Рис. Зависимость s is от s 0 характер изменения при испытаниях г:о схе (ВА) и Бокера

Во втором случае нагружение идет по линии СА, а всестороннее сжатие уменьшается от р _II до s_0А. Следовательно, при использовании разных схем нагружения можно получить различный характер нагружения и наиболее полно воспроизвести реальный процесс деформирования горных пород.

Влияние температуры, по данным Н. Н. Павловой, сводится главным образом к уменьшению предела текучести. Для большинства осадочных пород нагрев до 200°С приводит к уменьшению s _is на 15—20%. Для каменной соли предел текучести уменьшается в несколько раз.

Дата добавления: 2014-01-11