Параграф 3. Моменты силы относительно точки

Аксиома затвердевания

Аксиома связей (принцип освобождаемости)

Аксиома 5: Всякую несвободную НМС (МТ) можно рассматривать как свободную, отбросив (условно) связи и заменив их действие реакциями связи (пассивными силами).

Аксиома 6: Равновесие несвободной МС не нарушится, если на нее наложить дополнительные связи.

Пусть имеются сила , приложенная в точке какой-либо НМС, точка О и ось l. Тогда можно дать определения моментам силы относительно точки и оси и установить связь между ними.

Определение: Моментом силы относительно точки называется вектор, приложенный в этой точке, равный по величине произведению величины силы на кратчайшее расстояние от точки до линии действия силы (называемое плечом), направленный перпендикулярно к плоскости, проходящей через точку и силу, по правилу правого винта, т. е. в ту сторону, откуда совершаемый силой поворот тела, относительно точки виден против хода часовой стрелки (рис. 6).

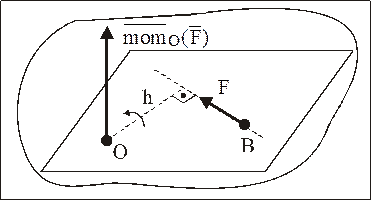
Рис. 6

. (1.1)

Введем в рассмотрение радиус-вектор , определяющий положение точки B – точки приложения силы (рис. 7).

Рис. 7

При рассмотрении векторного произведения векторов и , оказывается, что

а) ;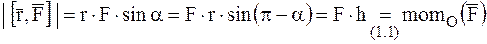

б) 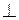плоскости, в которой находятся ;

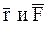в) составляют правую тройку векторов, т. е. если смотреть с конца третьего вектора, поворот от первого ко второму вектору виден против хода часовой стрелки.

Таким образом, можно сделать следующий вывод:

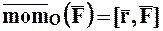. (1.2)

В случае плоской системы сил величину момента силы относительно точки, лежащей в плоскости действия сил, можно рассматривать как алгебраическую величину, равную взятому со знаком плюс или минус произведению модуля силы на плечо:

.

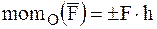При этом величина момента берется со знаком плюс, если сила стремится осуществить поворот тела относительно точки против хода часовой стрелки и со знаком минус в противоположном случае (рис. 8).

Рис. 8

Параграф 4. Момент силы относительно оси

Определение: Моментом силы относительно оси называется взятая со знаком плюс или минус величина момента проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси и плоскости:

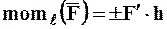. (1.3)

Момент берется со знаком плюс, если, смотря с конца положительного направления оси, видно, что проекция силы стремится осуществить поворот тела относительно оси против хода часовой стрелки. В противном случае момент берется со знаком минус (рис. 9).

Рис. 9

Момент силы относительно оси не зависит от выбора плоскости, перпендикулярной оси.

Момент силы относительно оси равен нулю, если:

· =0, т.е. сила параллельна оси,

· h=0, т.е. линия действия силы пересекает ось.

Дата добавления: 2014-01-13