КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение 2
|
|
|
|
Замечание
В механике дифференцирование по времени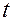 
принято обозначать точкой над функцией, от которой вычисляется производная. Согласно этому замечанию, равенство (В.5.1) принимает вид
.
Мгновенным ускорением (ускорением) материальной точкив момент времени 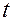называется производная от вектора скорости.
Ускорение точки, как правило, обозначается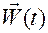 
. Так что (с учетом (В.5.1) и замечания к определению 1) можем записать
.
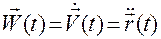2º. Скорость и ускорение механической системы и твердого тела
|
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 253; Нарушение авторских прав?; Мы поможем в написании вашей работы!