Основные понятия. Переходные процессы в линейных электрических цепях

Переходные процессы в линейных электрических цепях.

АНАЛИЗ ПЕРЕХОДНЫХ (ДИНАМИЧЕСКИХ) ПРОЦЕССОВ ВО ВРЕМЕННОЙ ОБЛАСТИ

3.1. Переходные процессы в линейных электрических цепях. Основные понятия

3.2. Классический метод расчета переходных процессов

3.2.1. Подключение катушки индуктивности к источнику постоянного напряжения

3.2.2. Отключение катушки индуктивности от источника постоянного напряжения

3.2.3. Включение катушки индуктивности к источнику синусоидальной э.д.с.

3.2.4. Заряд конденсатора от источника постоянного напряжения

3.2.5. Разряд конденсатора на резистор

3.2.6. Подключение конденсатора к источнику синусоидального напряжения

3.2.7. Разряд конденсатора на RL-цепь

3.2.8. Подключение RLC-цепи к источнику постоянного напряжения

3.2.9. Расчет переходных процессов в сложной цепи

3.3. Метод переменных состояний

3.4. Расчет цепи при воздействии э.д.с. произвольной формы. Интеграл Дюамеля

Переходный процесс – процесс, возникающий в электрической цепи при переходе от одного установившегося режима к другому.

Установившийся режим – режим, устанавливающийся в электрической цепи в результате длительного воздействия на эту цепь постоянных или периодических э.д.с.

Переходный процесс возникает в электрической цепи в результате коммутаций.

Коммутации – действия, вызывающие переходный процесс в электрической цепи отключение или включение источников, отдельных ветвей, изменение параметров цепи, изменение фазы, частоты, амплитуды напряжения и тока и др.

Задача анализа переходных процессов заключается в определении характера изменения u(t) и i(t) на элементах электрической цепи во время переходного процесса и длительности протекания этого переходного процесса.

Анализ переходных процессов основывается на описание состояния электрической цепи с помощью законов Кирхгофа для мгновенных значений. В результате получаем систему интегро-дифференциальных уравнений. Задача анализа переходных процессов сводится к отысканию решения (интеграла, интегрированию) исходной системы уравнений.

Пример:

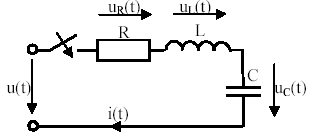
В зависимости от используемого метода интегрирования различают:

1) классический метод анализа переходных процессов;

2) операторный метод анализа переходных процессов;

3) частотный метод анализа переходных процессов;

4) метод с использованием интеграла Дюамеля;

5) метод переменных состояния.

Законы (правила) коммутации

Будем полагать, что процесс коммутации происходит мгновенно (хотя реально – это микросекунды для тиристоров, транзисторов).

Условно обозначать через t=0 – момент коммутации

t = 0_– – момент времени непосредственно до коммутации;

t = 0₊ – момент времени непосредственно после коммутации.

В реальных электрических цепях не может быть мгновенного изменения накопленной в электрических и магнитных полях энергии.

Действительно, в реальных электрических цепях мгновенная мощность p всегда конечна (т.к. u и i конечны). Следовательно, прирост энергии DW за время коммутации D tÞ 0равен 0:

DW = рD t Þ0, при D t Þ0, т.е.

W(0_-) = W(0₊).

Таким образом:

1-е правило коммутации. Ток в ветви с катушкой индуктивности не может изменяться скачком:

2-е правило коммутации. Напряжение на конденсаторе не может изменяться скачком:

Или:

В момент коммутации напряжения на конденсаторах и токи в катушках индуктивности остаются неизменными.

Пример:

Дата добавления: 2014-01-13